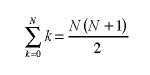The Mathematics of Carl Friedrich Gauss (1777-1855) (German)
 |
|
It is said that Gauss was able to calculate before he could even talk.
It is known that he corrected his father's error in calculating wages. He
possessed a scientific and classical education far beyond his fellow
schoolmates. The story goes that, in his first arithmetic class,
eight-year-old Gauss astonished his teacher by instantly solving the
problem of finding the sum of the first 100 integers. He used the formula:
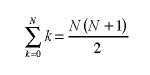 where N is equal to 100 in this case. where N is equal to 100 in this case.
|
Gauss came from a poor family. His father was an odd
job worker. However, he was a lucky man. Recognizing his talent, the teacher
actually went through some pain to promote it. Later, the Duke of Brunswick
asked to see Gauss and took him in, sponsoring all his researches and thereby
allowing him to concentrate on Mathematics and Physics. However, the Duke died
1806 at war and hence Gauss had to find a job, which he obtained as the director
of observatory at G�ttingen University in
1807. He had himself studied there in 1795-8. He stayed there till his death in
1855. When Napoleon conquer Germany, he spared the city of G�ttingen
because the greatest mathematician of all time is living there. He died
of heart attack while sitting in his G�ttingen
chair. At his
death, the King of Hanover ordered a commemorative medal with the title "Prince
of Mathematics" on it. Gauss' brain was preserved and stored in the
university's physiology department till this day.He was familiar with elementary geometry, algebra, and
analysis. He often "discovered" important theorems before encountering them in
school. In addition, he possessed a wealth of arithmetical information and many
number-theoretic insights. He alone "discovered" Bode's law of planetary
distances, the binomial theorem for rational exponents, and the
arithmetic-geometric mean, just to mention a few. At the age of 24 he published
Disquisitiones Arithmeticae, one of the most brilliant achievements in
the history of Mathematics. It's a classic on Number Theory. As the amount of work he produced was enormous and
extends into almost all fields of Mathematics, I'll describe only the prominent
few here.
1. Law of Quadratic Reciprocity
This law was conjectured by Lagrange in
1785 and it is one of the most important discoveries in Number Theory. Before
entering the University of G�ttingen in 1795, Gauss had already rediscovered
this law. This is one of his favourite theorems and he produce several proofs
for it over his lifetime.
Let p and q be odd primes, then
where
He conjectured the prime number theorem, which
was first proved by J. Hadamard in 1896. Let
π(n) be the number of
primes less than or equal to n. For large n,
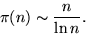
This is a most extraordinary theorem
because for once we have a means of knowing how sparse the prime numbers are
without having to directly count the number of primes.
History has it that Gauss often discover important results without publishing
them, but when someone discover the results later and publish them, he would
mention that he had already discovered them years before. Hence it appears that
anytime someone published a result in the first half of the19th century, Gauss
would have already thought of it. Such was the case for the Prime Number Theorem
(PNT). In 1792, Gauss worked out the number of primes in blocks of 1000 natural
number up to a million, and from that deduced the PNT. However, he did not
publish the result. Then in 1798, Legendre (1752-1833) published in his
book Essay on the Theory of Numbers, the PNT in the form
π(x) ~ x / (Alnx + B),
where A and B are some numbers to be determined. In a later
edition he wrote A=1 and B ~ -1.08366. Gauss wrote in 1849 demolishing the
values of 1.08366. Fortunately for Legendre, he had died in 1833. In another
example, it wasn't so fortunate for him. It was discovery of the least square
method in his 1809 book, which Gauss claimed he discovered in 1794. Gauss'
claims can be verified with documentary proofs.
3. Fundamental Theorem of Algebra
Gauss provided the first proof of this
important theorem in 1799. The theorem states that a real-coefficients
polynomial equation of degree n has exactly n roots. Some of these roots can be
equal.
4. Non-Euclidean Geometry
He is one of the founders of non-Euclidean
geometry. Like the other founders of non-Euclidean geometry, he discovered this
geometry while trying to prove the parallel postulate:
Given any straight line and a point not on it, there "exist one and
only one straight line which passes" through that point and never intersects the
first line, no matter how far they are extended.
What is
happening here is that there are 5 axioms that form the basis for Euclidean
geometry and the fifth axiom (the parallel postulate) is more complicated than
the other four. So Mathematicians since Euclid have tried to prove it from the
other four axioms. However, it is found that if the parallel postulate is
assumed to be false, we can still get consistent geometry (the non-Euclidean
geometry), thereby showing that it is not provable from the other axioms.
5. Construction of 17-gon by ruler and compass
In 1796 came a dramatic
discovery that marked him as a mathematician. As a by-product of a systematic
investigation of the cyclotomic equation (whose solution has the geometric
counterpart of dividing a circle into equal arcs), Gauss obtained conditions for
the constructability by ruler and compass of regular polygons and was able to
announce that the regular 17-sided polygon (17-gon, in short) was constructible
by ruler and compasses. In fact, he proved a much more general theorem: that the
necessary and sufficient condition for the constructability of regular polygons
are that the number of sides must be a power of 2, a Fermat prime, or a product
of these numbers. Fermat Numbers
are numbers of the form:
Fn =
22n + 1, where
n is a non-negative integer.
If this turns out to be a prime, it is called a Fermat prime. These numbers
were first mentioned by Pierre de
Fermat. This discovery was so important to him that he wanted a regular
17-gon to be constructed on his tombstone.
6. Electric Telegraph
Gauss together with Weber invented the electric telegraph.
Other accomplishments
There are many theorems, not only within
Mathematics, but also within Science as a whole, which are named after Gauss. A
few are mentioned here:
Gaussian Elimination (a neat program to do this can be found at Matrix Solver).
Gauss-Siedel iteration
Gauss' Theorem
(this helps to reduce a volume integral into a surface integral)
Gauss' Law
(of Electric Field)
Gauss' Law of Magnetics
Gaussian distribution (the
bell curve)
Gaussian integers (a+bi, s.t. a and b are integers and
i is the
square root of -1)
Gaussian plane (the complex number plane)
Gaussian
quadrature (a method for approximating integrals)
Short notes on some of the mathematicians mentioned in this page.
1. Adrien-Marie Legendre (French) died in poverty. His Elements of
Geometry was the elementary text on the topic of a century and is said to
inspire Galois to take up a career in Mathematics.
2. Wilhelm Weber (German) was a physicist. Like Gauss, he taught at the G�ttingen
University.
Return to Maths
Homepage Homepage