Mathematical Exercises
Mathematical Exercises (MEs) are not the typical
exercises found in textbooks. They are problems which are related to the topic
to be taught, but which are not necessary for the understanding of the topic
itself. They are more for stimulating mathematical thoughts and making the
lesson interesting. They need not be fixed questions detailed to students by the
tutor, but could be anything the tutor (or even the students) think of that
relates to the topic at hand.
Example 1
For example, after studying the topic on 'Hyperbolic
Functions', the tutor can ask the students to create a 'Generalized Hyperbolic
Functions' and ask questions like 'What's the consequence of doing so?' or 'Is
the generalization helpful?'. You'll be surprised what the students can come up
with. A possible generalization would be to replace the e in coshx
= (ex + e-x)/2 by any constant
real number, a. We denote this by cospx (the tutor can ask the
students to come up with their own notations). A consequence of this is that on
differentiation, we have D(cospx) = sinhxlna. This results
in the extra term, lna. So it does not seem helpful at all to generalized
the function in this way. What about the identity cosh2x -
sinh2x = 1? Is it affected? A short exercise would show that
the identity is preserved.
What the students gain from this exercise is that they learned about
generalizing problems in Mathematics, which is one of the ways Mathematics
develop, and in some case we get to know more about the specific problem at hand
by looking at a more general form. However, in our 'pyperbolic' case,
generalization does not really help at all, but this does not defeat the purpose
of the exercise. It just goes to show that not all generalizations are useful.
Furthermore, students may think of other more interesting ways of
generalization, which certainly serve the purpose of arousing their thoughts.
Another interesting aspect of this exercise is that students get to understand
more of Hyperbolic Functions, because in working out D(cospx) and
verifying the identity still holds, they need to work through the very proofs of
D(coshx) and the original identity.
Example 2
If you are teaching a topic on graphs and special functions
(exponential, trigonometric, logarithmic, etc), you could ask students to think
of new functions and try to study these new functions in depth. One possibly
interesting function to work at would be y = xx. How does the
graph look like? Is it continuous? Does it have any special features? Is it a
function at all? Students can use a brute force method, by plotting many point
on a piece of graph paper to visualize the curve, or they could use standard
softwares to generate the graph, or they could employ Analysis to understand it
more thoroughly. You'll be surprised by the multitude of ways they can think of
to approach the problem.
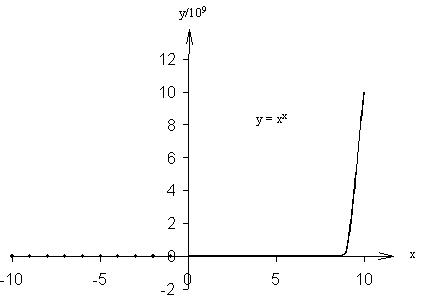 |
It is a function alright and it has many interesting features. It is
not continuous over the whole domain of x. In fact, it is only continuous
for x > 0. It is not defined at x = 0 and also for many
negative x values. One feature that is not obvious from a plot of
the curve (if you use a large domain of x) is that there is a minimum
point at x = 1/e = 0.3678... The reason being that the curve
around this point is quite gentle. The exact value of 1/e can only
be obtain via Analysis and not through curve-plotting. All these
subtleties should be raised to the students doing the exercise.
|
Here's the Analysis:
| y = xx |
=> lny = xlnx |
|
=> y'/y = 1 + lnx |
|
=> y' = xx(1 +
lnx) |
Now y' = 0 => 1 + lnx
= 0 => x = 1/e = 0.3678...
It is easy to verify that
y"(1/e) > 0, showing that it is indeed a minimum point.
Also from
the graph, it seems that y is 0 at all negative values that the function
is defined, but we know that it is just that the y values are very small
(particularly for the more negative x).
Example 3
Not all MEs need to be about new stuffs. Another useful ME is
to ask students to generate their own proofs of known theorems. One top
contender would be Pythagoras Theorem. There are virtually hundreds of proofs of
this famous theorem out there. It does not matter that the proofs the students
thought of are already in the literature (which is most likely the case), what
matters more is that they really think of a proof. The proof need not be one
they have never seen before. If it is one they read in a text, it serves to
consolidate their understanding of the theorem. Another important aspect of this
ME is that the idea of a proof is instilled in the minds of the students. The
importance of proofs is in the mind of all mathematicians and it is necessary
that amateur learners of Mathematics also have the same mentality.
Example 4
Also suitable as MEs are unsolved problems in Mathematics. Of
course the aim is not to solve these problems at all (if that happens it would
really be a bonus!). Many times new branches of Mathematics blossom from studies
on unsolved problems. An example is Henri Poincar�s discovery of Chaos Theory
while working on the Three-Body
Problem. A great contender for this category of MEs is Fermat's Last Theorem
(although FLT is no longer an unsolved problem). Many great mathematicians have
worked on it through the 350 years since it's formulation by Pierre de
Fermat. What's interesting about it is not just that many new Mathematics is
created but also that many fallacious 'proofs' have been submitted through the
ages. The students could be taught to recognize mistakes in 'proofs', by
presenting them with fallacious 'proofs' (some of which may come from the
students themselves) and asking them what's wrong with the logic of the
'proofs'.
My favourite example is a fallacious proof of FLT, which goes like this:
Assume an + bn = cn
and r is a natural number.
Let a>b.
| Now an+r + bn+r
| = aran +
brbn
|
|
| = ar(cn - bn) +
brbn
|
|
| = arcn + (br -
ar)bn
|
|
| = cn+r + (ar -
cr)cn + (br -
ar)bn |
Since c>a, we have
cr>ar or ar -
cr<0.
Also b<a, we have
br<ar or br -
ar<0.
Thus an+r +
bn+r != cn+r.
Since when n=2, we have a2 + b2 =
c2, this means for higher exponents (m>2),
am + bm != cm (QED)
The error here is not in the logic of the statements, but rather the wrong
interpretation of the proof. What is being proven here is simply that
Pythagorean Triples cannot be Fermat Triples, and not that FLT is proven true.
Example 5
Of course we should not forget puzzles as the traditional
means to get students interested in Mathematics. They work most of the time.
Since old days, children have indulged themselves in tic-tac-toe, Sam Lyod's
15-puzzle, etc. And presently, the computer game available on all PCs,
Minesweeper, has been adopted by certain institutions to stimulate logical
thinking. All these games involved a certain set of simple rules and players
need to make logical deductions to achieve the goal, while adhering to the
rules. Instead of just playing the games, students can be asked to analyze the
strategy of the games. The simplest to start off is tic-tac-toe. Ask them to
come up with a sure-win strategy, if it exists. Ask them whether it is possible
to ensure that the opponent never wins.
Such an exercise introduces students to topics they will most probably not
encounter until they reach University level and choose to major in these topics.
Analysis of strategies in games and puzzles belong to Game Theory, and students
are not likely to learn it unless they major in Mathematics or Economics.
Exposing students to a wide range of mathematical concepts is essential for
all-round education, as all branch of Mathematics find applications in the real
world. The answer to the questions posed for tic-tac-toe is that there is no
sure-win strategy, but you can always prevent the opponent from winning (by
forcing a draw).
Example 6
Another form of ME is speed calculation. How do we make
calculations without pen and paper or a calculator? There are a few tricks. We
can do addition, simple subtraction, doubling and halving very quickly mentally.
By breaking down a sum into these simple steps, we can make seemingly tough
calculations without any tool. Take for example the conversion from Fahrenheit
to Celsius. The formula is C = 5/9 (F-32). How can we make this conversion
mentally? Observe that we can rearrange the formula to C = 10/9 * 1/2 * (F-32) =
1.111... * 1/2 * (F-32). Let x = 1/2 * (F-32), hence C = 1.111... *
x = x + 0.1*x + 0.01*x + ... This might look like
we're getting nowhere. But this is actually easier to see with an example: e.g.
F=60.
| step1:
| 60-32=28
|
| step2:
| 28/2=14
|
| step3:
| 14
|
|
| +1.4
|
|
| +0.14
|
|
| +...
|
|
| =15.55555... |
It might not appear easy at first glance but after a few examples, the
algorithm become second nature to apply. Now, what's the algorithm for the
conversion from C to F? Try it.
Example 7
The examples of MEs could go on and on, they are just limited
by your imagination, so I'll just present another one here. This one arise from
exercises in a textbook on Elementary Geometry. As we all know there are many
Circle Theorems in Geometry. The number of such theorems need not be limited to
those presented in the book, you can create your own ones. Here is it:
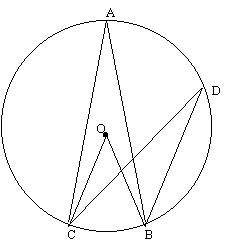 |
I am going to show that ^OBA + ^OCA = ^BAC and that ^OBD - ^OCD =
^BDC. These can be combined together as a single theorem if we adopt a
suitable convention, so that the second equation becomes ^OBD + (-^OCD) =
^BDC. I call the result "Sum of Side Angles".
The first equation follows from the fact that triangles OAC and OAB are
both isosceles. Similarly, the second equation depends on triangle OCD and
OBD being isosceles. |
So much has been said, but what really matters is action. Just let our
imagination run wild and think of interesting MEs to uncover mathematical
talents!
Return to Maths
Homepage.


