Additive
One way to improve on the unary system is to group a
certain number of strokes and give it a new symbol. E.g. @ = 5 strokes, then
@@||| = 5+5+1+1+1 = 13. Before the use of cuneiforms, the Sumerians used an
additive sexigesimal (base 60) number system that has symbols for 1, 10, 60,
360, 3600, 36000. The Egyptian Hieroglyphic is also additive, but it is base 10.
| 1 | 10 | 100 | 1,000 | 10,000 | 100,000 | 1,000,000 |
|
|
|
|
|
|
|
The hieroglyphic requires too many symbols to write a number, so for purpose of calculation, another system was developed, namely the Egyptian Hieratic. This is also an additive decimal system, but it has symbols for 1-10, 20, ..., 100, 200, ..., 1000, 2000, ..., 9000, altogether 36 numerals. Hence only 4 numerals are needed to write the number 5629 in hieratic, compare to 22 in hieroglyphic. Drawbacks of this system is that there is no way to write numbers larger than 9999 and there are too many numerals to remember, but bear in mind that this system was developed to simplify calculation; the final result of the calculation would still be written in hieroglyphic. And for daily calculations, there was probably no necessity to go beyond that.
The Egyptians is believed to adopt a decimal system based on the fact that we have 10 fingers. It is pretty intuitive to use our fingers to count, as is evident from young school pupils starting to learn arithmetic. Why then did the Sumerians not adopt a decimal system? There are many theories to explain this. Some say that 60 is used because it divides evenly into 2, 3, 4, 5, 6 and this is important because they dealt with fractions regularly. All their fractions are reciprocals of natural numbers, except for two special cases: 2/3 and 3/4. Some say that it is based on approximately 360 days per year, even though the Sumerians know that there are more than 360 days per year. It is not surprising because approximations are constantly used throughout history for practical purposes. E.g. for ease of computation, sometimes π is taken as 3 by the Babylonians. Yet another explanation is that our fingers have 3 sections separated by the joints, except the thumb of course. By pointing any of the 5 fingers of the left hand on any of the 12 sections on the right hand, we can count to 60. Regardless of the reason for a sexigesimal system, the intuitive idea of using the 10 fingers on each hand is still observable with the sexigesimal system because of a numeral for 10. How it was extended to 60 and not 100 is still a mystery.
The evolution of the Greek number system is similar to the Egyptian, i.e. they had a system that was like the hieroglyphics (ancient Greek system) then they adopted another system like the hieratic (learned system). The ancient Greek system has symbols for the different orders of 10 as well as for 5, 50, 500, 5000, 50000. The learned system has symbols for 1-10, 20, ..., 100, 200, ..., 900. The symbols for 1000, 2000, ..., 9000 was created by prefixing the symbols for 1-9 with a superscripted or subscripted symbol for 10. The symbols for 6, 90 and 900 were obsolete and that is why now there are only 24 Greek alphabets.
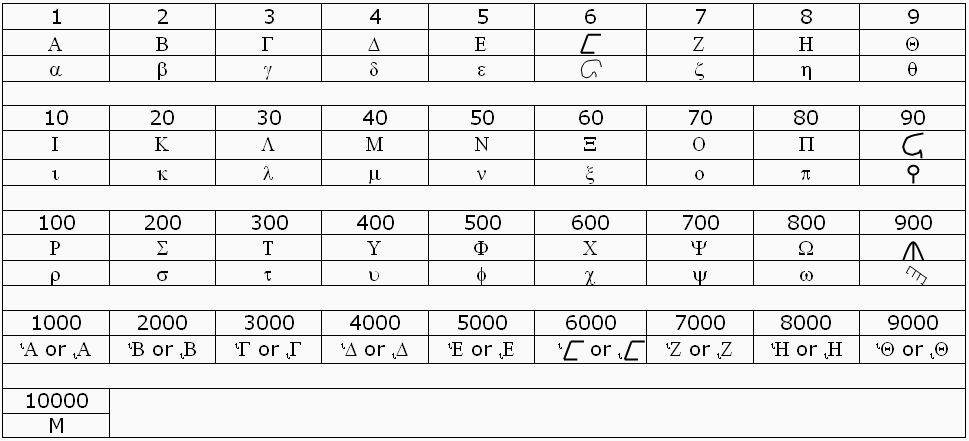
There were different ways to write numbers larger than 19999. The earliest preserved the additive property by putting a beta b on top of the myriad M to represent 20000 and so on. Apollonius developed a better approach later and it is an additive-multiplicative system (more about this later). In this case, b over M represents M2 = 108.
Even today we use additive systems in our daily life: the currency we use. In the US, we have the denominations: 1-cent, 5-cents, dime (10 cents), quarter (25 cents). Suppose we give them the symbols:
| | | = 1-cent |
| @ | = 5-cents |
| # | = dime |
| $ | = quarter |
Multiplicative-additive
A variant to the additive system is the
multiplicative-additive system. The English and Chinese systems are
multiplicative-additive decimal systems. E.g. two hundred and four = 2�100+4 =
204. The English and Chinese systems are actually pretty similar, they have
words for 1-10, 100 and 1000. They differ from there onwards. The Chinese have
words for 10000 and 100002, whereas the English have words for
10002. The English has words for larger numbers but there is a
difference between the US English and the UK English system in that the US has
words every 3 orders up, whereas the UK has words every 6 orders up. E.g.
billion is 109 in US but is 1012 in UK.
Subtractive-additive
Yet another variant is the
additive-subtractive system of the Roman numerals. The symbols are I=1, V=5,
X=10, L=50, C=100, D=500, M=1000. VI = 5+1 = 6 but IV = 5-1 = 4.
All these systems are non-positional and therefore there is no need for a symbol for zero.
Sexigesimal
The Sumerian cuneiforms
was the first positional
system. However, it is sexigesimal and it does not have a symbol for zero. The
unique feature is that even though it is sexigesimal, it has only 2 symbols.
They used a stylus to carve the numbers on clay tablets and the result is
wedge-shaped symbols. In their symbols, 
=
1 and 
= 10. We will write sexigesimal
numbers in this notation: 1,16,10 = 1�602 + 16�60 + 10. In
cuneiforms, this is
. The
main problem with this system is that there is no symbol for zero, so there is
no way to tell the difference between 1,16,10 and 1,0,16,10 or 1,16,0,10, etc.
They did leave a space between digits to represent zero, but this will cause
ambiguity because if the space is too small you can miss a zero and how much
space must be left if there are two consecutive zeroes? It was only at 400BC
that they developed a symbol of zero, but there is only evidence to show that
they use it between digits; they didn't use it at the end of the number. This
goes to show that they did not treat zero as a number, but rather as a
punctuation. The other problem is there are too many wedges to draw. Imagine
having to draw 9 and 5
for the number 59. The cuneiform sexigesimal
system is of course no longer in use, but we can still see remnants of it from
the way we tell time, e.g. 5 hours, 45 minutes and 2 second = 5 45' 2".
Binary
The first binary system was not even additive. It is called
the one-two-many system. In this system, there are only words for one, two and
many. Anything more than two is known as many. This is hardly a number system.
And yet it is still in use by some primitive tribes in Africa and South America.
One example is the Pirah� tribe of Brazil. They could distinguish between 1, 2
and 3, but anything more they could not distinguish. One reason is that there is
no necessity to count to numbers larger than 3, so they never develop a system
to do so. In cultures that need to count larger numbers, the two-count system
was founded. This is an additive binary system. Let 1 = one and 2 = two, then to
count the number 5, they say "two two one" (2-2-1). The positional binary system
is the binary system we are familiar with now. It is used in computer
programming because electronic circuits only have 2 states: on (1) or off (0).
In binary notation, 10 is actually two in decimal. We write this as
102 = 210, where the subscript is the base used. In
general,
(anan-1...a1a0)2 = (an�2n + an-1�2n-1 + ... + a1�21 + a0)10,
where the a's are either 1 or 0. In order to represent the binary numbers more efficiently, sometimes hexadecimal (base 16) numbers are used. E.g. (10001010)2 = (8A)16, where A=10 in decimal. In hexadecimal, 16 digits are needed, namely 0-9, A-F, where A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
Decimal
The present decimal system we are using is called the
Hindu-Arabic system. That is because the Hindu Indians were the first to develop
this system using the Brahmi numerals. The Brahmi numeral system was an additive
system. The nine digits 1-9 of the Hindu-Arabic system developed from the Brahmi
numerals. It was then through the Arabs that it spread to Europe and the rest of
the world. However, the story could be more complicated than this because the
Chinese had a positional decimal system before the Indians developed theirs and
it could be more than coincidental that the spread of Buddhism between the two
regions occurred at the same time the Indians came up with the positional
decimal system. In any case, by 500AD the Indians had their own positional
decimal system without zero. Soon, it has spread to the Arabs. It is known that
the Indians had a word for zero and had used a dot to denote an empty space
before the symbol of zero came into their system. Brahmagupta (600-670AD)
was the first to treat zero as a number and wrote the arithmetic of zero out in
full, although he had some difficulties with division involving zero. al-Khwarizmi (780-850AD)
was amongst the first to write a treatise on
the Hindu-Arabic system with zero. By 876AD, both the Arabic and Indian systems
had a symbol for zero. It was Leonardo Fibonacci (1175-1250) who brought
this system into Europe. In his 1202 book Liber Abaci, he introduced the
Hindu-Arabic system to the western mathematical community.
Other Bases
The general formula to convert base m to
decimal is
(anan-1...a1a0)m = (an�mn + an-1�mn-1 + ... + a1�m1 + a0)10,
where the a's are numbers from 0 to m-1.
The Mayan of South America used a vigesimal (base 20) system.
Short notes on some of the mathematicians mentioned in this page.
1) Brahmagupta (Indian) not only contributed to the Hindu-Arabic
system, but also to Astronomy, Diophantine Equations, Algebra.
2) al-Khwarizmi (Arab) wrote the treatise Hisab al-jabr w'al-muqabala
on Algebra in 825 which eventually gave us the word 'algebra'. He also contributed to
Arithmetic, Astronomy, Geography.
3) Fibonacci of Pisa (Italian) is
known to all for his Fibonacci Sequence, which was described in Liber Abaci. His
other major contribution is to Number Theory with the book Liber
quadratorum.
Return to Maths Homepage