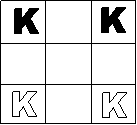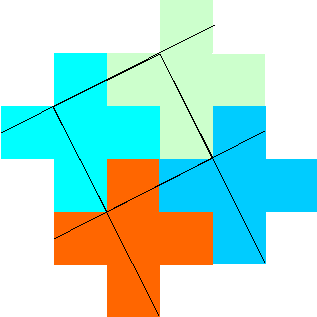Recreational Mathematics
Puzzles involving shapes and
figures
|
Many puzzles and games are mathematical in nature. Sam Loyd
(1841-1911) is a famous
recreational mathematician. He's considered the greatest American creator of puzzles.
The only contender for the greatest world creator of puzzles is
Henry Ernest Dudeney. However, his puzzles never appeared in book during his lifetime, except in
newspapers and magazines. It's after his death that his son, Sam Lyod Junior,
compiled his works into the Cyclopedia of Puzzles (1914). Amongst his greatest invention is the 15 Puzzle or
Sam Loyd's Boxes, which he created in 1878. It's played by messing up the order
first and then attempting to rearranged it back to order. The numbers can only
be slided in the plane and can't be lifted.
(1) Is it possible to rearrange the puzzle so that 14 and 15
are interchanged?
Give it a try before going to the answer at the bottom. |
| 1 |
2 |
3 |
4 |
| 5 |
6 |
7 |
8 |
| 9 |
10 |
11 |
12 |
| 13 |
14 |
15 |
|
|
| |
Sam Loyd's Boxes or 15 Puzzle
|
|
Another group of puzzles include dissecting and rearranging
a shape to form another shape. Take for example this cross made up of 5
squares of equal size. (2) How do you dissect it with 2 straight
lines to form a square? (Hint: use tessellation). Other such puzzles can be
solved by sawing or stripping.
|
 |
Another type of dissecting puzzle does not involve rearranging. E.g.
(3) what
is the maximum number of regions that can be obtained with 7 straight line
dissecting a circle?
Paper-folding is also an entertaining mathematical game. Origami is the art
of paper-folding, which allows us to fold a plane sheet of paper into a
three-dimensional object, like a crane, a jackstone, etc. The proof that origami
is a mathematical art can be seen in the fact that there is even a function in
Mathematica for origami! We'll not go into origami per se, but will take a look
at simpler paper-folding games. (4) What is the largest equilateral triangle
that can be folded from a plane sheet of square paper? No markings/measurements
allow on the paper.
| Graph Theory also has its place in mathematical recreation. Try drawing the
figures below without lifting your pen from the paper or retracing any line. |
 |
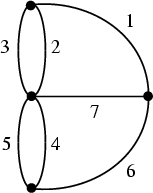 |
| Figure
(5a) |
Figure (5b) |
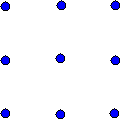
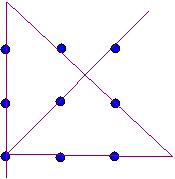
| (6) Draw 4 straight lines through the 9 dots without lifting your pen from
the paper. |
 |
|
(7) Matchstick puzzles involve moving/adding/removing matches to achieve
certain configurations.
For the figure on the right,
(a) Move 2 matches to make 6
squares;
(b) Move 4 matches to make 10 squares;
(c) Remove 2 matches to make 2
squares.
|
 |
Dominoes can be considered as 2 squares joined together to form a rectangle.
The number on each square is from the set {0,1,2,3,4,5,6}and are represented by
the number of dots rather than the numerals themselves. There are 28 distinct
permutations. Consider a subset of this set of 28 consisting of the 6 dominoes
0-0, 0-1, 1-1, 0-2, 1-2, 2-2. (8) How do you arrange these 6 dominoes to form a
rectangle which adds up to the same number of dots on each side of the
rectangle?

Because dominoes come in 2 colours, it is sometimes mixed with a chessboard
to form a bigger set of puzzle. The typical chessboard is an 8X8 checkered
board. (9)(a) If the 2 white corner squares are
removed, is it possible to tile the board with dominoes? (b) What about if the
squares marked A and B are removed?
|
(10)
Consider a constrained chessboard with only 9 squares. How
can the black knights and white knight exchange position using the rules of
chess, i.e. knights move in an L-shape?
|
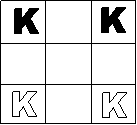 |
Suppose the dominoes are extended to form trominoes (3 squares), how many
possible tromino configurations are there? There are 2. Rotation is allowed. How
about tetrominoes (4 squares)? There are 6. 5 if flipping is allowed.
(11) How many pentominoes (5 squares), assuming
both rotation and flipping are allowed? Those who have played the game of Tetris
will be familiar with these shapes. The game involves such shapes dropping down
from the top and the player has to determine where to place the shapes so as to
clear these shapes at the bottom. The way these shapes are cleared depends on
the rules: it could be 3 or more squares forming a straight line; these squares
may have to be of the same colour; diagonals may be allowed.
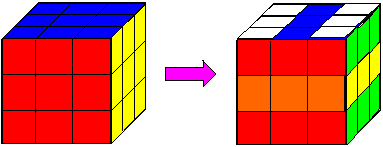
Rubik's Cube was very popular game in the 1980s. It's a cube made up of 27
smaller cubes of the same size and has 6 different coloured faces.
(12) How do you get from the plain cube to the
configuration on the right?
Now we move from puzzles involving shapes and figures to word puzzles.
Next Page.
Answers:
(1) It is impossible to rearrange the 15 Puzzle so that 14 and 15 are
interchanged. This is due to the theorem that only arrangements that have an
even number of interchanges has a solution.
(2)

This one can be solved by tessellation.
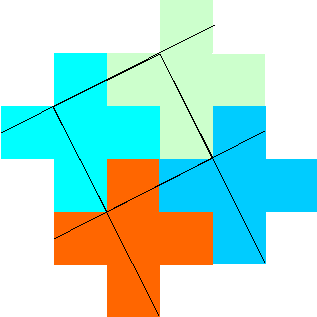
(3) 29. The answer follows the formula n(n+1)/2 + 1, where n
is the number of straight lines. How is this formula obtained (Hint: every new
line added must cut all previous lines) and is it still valid for large values
of n?
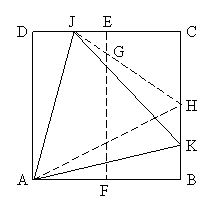
(4) Fold the square in half to make crease EF. Fold AB so that B lies on EF.
This gives points G and H. Fold HGJ. While B is on G, fold AB back to AH to get
K. AJK is the largest equilateral triangle (prove this).
(5) Part (a) has a solution, but there is no solution to (b). (b) is the
famous Konigsberg Bridge Problem (see
Euler). There
is only solution to such problem if there are at most 2 vertices with odd number
of lines and one of the odd-numbered vertex will be the start, while the other
will be the end (if there are 2 of them).
(6)
(7)
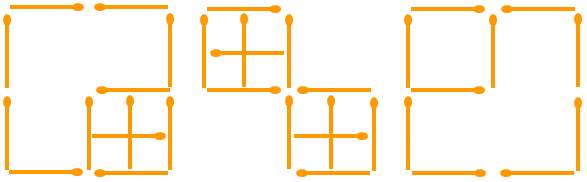
(a)
(b)
(c)
(8)

(9) (a) It is impossible because there are more black squares than white
ones. Reason: each domino spans across 1 black and 1 white square. (b) Yes. As
long as A and B does not cut the spiral into any section with odd number of
squares.

(10) It can be achieved after 4 clockwise (or anti-clockwise) moves for each
knight.
(11) 12.
(12) Apply 180o turns to the following faces: front, right, back,
front, right, back.