|
Euclid of Alexandria is well-known for his great work, The Elements, which is a compilation of all the Geometry of his time. However, Euclid's effort is more than just a simple compilation of previous works. It is the first systematic approach to Geometry; the first axiomatic approach of its kind. Although usually associated with Geometry, The Elements also contained some works on Number Theory. Although, the formal system advocated by Euclid is incomplete, for the majority of us Euclid's Geometry is good enough, because it is simple yet concise. In the 20th century, David Hilbert completed the system by increasing the number of axioms from 5 to 20, and proved that the resulting system is complete and consistent. However, Euclid's effort cannot be underestimated. In fact, The Elements remained the Geometry text for 2000 years and is still used because of its simplicity. And it is the fifth postulate of The Elements that sprout the various non-Euclidean Geometry known to us now. |
Book 1
This book contained the preliminaries to all the other
books. There are 23 definitions regarding what is a point, line, angle, circle,
triangle; and what is meant by perpendicular, parallel, obtuse, acute, right
angle. There are 5 postulates from which the various theorems of The
Elements were deduced.
| Postulate 1: | It is possible to draw a straight line between and two given points. |
| Postulate 2: | It is possible to produce a finite straight line indefinitely. |
| Postulate 3: | It is possible to draw a circle given any point and radius. |
| Postulate 4: | All right angles are equal to each other. |
| Postulate 5: | If a straight line is drawn to intersect two given straight lines such that on one side (side A) of the straight line, the sum of the interior angles are less than two right angles, then the two given straight lines when produced indefinitely meet on side A. |
| On top of these postulates, there are 5 more axioms (which Euclid called Common Notions), which related to things like equals plus (or minus) equals must be equal; the whole must be greater than the parts. From all these definitions and axioms, Euclid deduced 48 propositions in Book 1. Some of the propositions has to do with the possibility of Straightedge and Compass Construction (SCC), e.g. Proposition 1 showed that it is possible to construct an equilateral triangle on any finite straight line. Others deal with the basic properties of triangles, parallelograms and parallels, e.g. Proposition 20 is the Triangle Inequality. Book 1 culminated with the famous Pythagoras Theorem (a2 + b2 = c2) as Proposition 47 and 48. |  |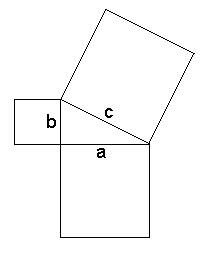
Book 2
This book starts off with two definitions with regard to
parallelograms and describes 14 propositions relating to triangles, rectangles
and squares. In particular, they are mainly the geometric equivalent of certain
algebraic identities, e.g. Proposition 2 is equivalent to the identity (a +
b)2 = a(a + b) + b(a + b) and Proposition 4 is essentially (a
+ b)2 = a2 + 2ab + b2. Proposition 12 and
13 together form the well-known Cosine Rule.
 |
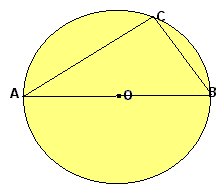Book 3 There are 11 definitions and 37 propositions with regard to circles. These include the Circle Theorems all students learn during elementary Geometry class. The diagram on the left illustrates the first part of Proposition 31, that if AB is the diameter, then angle ACB is a right angle. Book 4 |
Book 5 - 6
Book 5 is Eudoxus' Theory of Proportion, and there are
18 definitions and 25 propositions in it. Book 6 is also on Proportions, but in
it, the theory found application to figures (similar figures) and angles. Book 6
contains 4 definitions and 33 propositions.
Book 7 - 9
These are the only 3 books in The Elements that
dwell on Number Theory. The 22 definitions in Book 7 give rise to 102
propositions altogether (39 in Book 7, 27 in Book 8, 36 in Book 9). The
definitions of Even and Odd Numbers, Primes, Squares, Cubes, Perfect Numbers are
due to the Pythagoreans. As are many of the theorems. Book 7 contains a loose
version of the Fundamental Theorem of Arithmetic (Proposition 32). This theorem
states that any Natural Number can be factorized uniquely into Primes, but the
one in Book 7 does not assert the uniqueness. In Book 8 can be found the famous
proof of the infinitude of Primes (Proposition 20). Book 9 culminates in the
general formula for Perfect Numbers (Proposition 36). Again it is a loose
version, as it does not assert that these are the only Even Perfect Numbers.
Book 10
There 16 definitions and 115 propositions. The concept of
Rational and Irrational Numbers are introduced here. Rational Numbers are those
expressible as ratios of Natural Numbers, while Irrational Numbers are those
which are not. The famous proof of the Irrationality of
√2 can be found here.
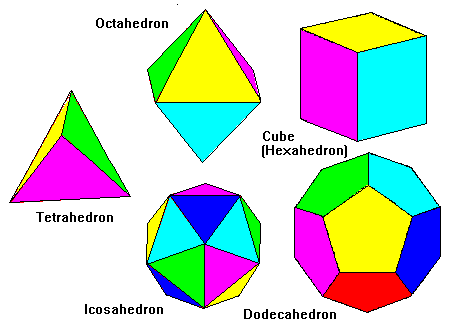
| Book 11 - 13 The 28 definitions give rise to the 39 propositions in Book 11, and 18 propositions in each of Book 12 and 13. They are concerned with Solid Geometry. In particular, Book 13 dwells on the 5 Platonic Solids, which are the only solids with all faces of the same shape. |
 |
For a complete (Java-applet) illustration of The Elements visit this
website:
Euclid's Elements
Return to Maths Homepage