Era of Greek Mathematics

The Greeks are responsible for the initial explosion of Mathematical ideas. For several centuries, Greek mathematics reign the mathematical world, with great advances in Number Theory, the Theory of Equation, and in particular Geometry. The first great Greek mathematician is Thales of Miletus (624-547 BC). He brought the knowledge of Egyptian Geometry to the Greeks and discovered several theorems in elementary Geometry. He predicted a Solar Eclipse in 585 BC and could calculate the height of a pyramid, as well as how far a ship is from land. One of his pupils, the Greek philosopher, Anaximander of Miletus (610-546 BC), is considered the founder of Astronomy.

Perhaps the most prominent Greek mathematicians is Pythagoras of Samos (569-475 BC). His ideas were greatly influenced by Thales and Anaximander. His school of thought practiced great secrecy and he (and his followers, called Pythagoreans) believe everything in the world can be reduced to numbers. This idea stemmed from Pythagoras' observations in Music, Mathematics and Astronomy. E.g. Pythagoras noticed that vibrating strings produce harmonics in which the lengths of the strings are in ratios of whole numbers. In fact, he contributed greatly to the mathematical theory of music. He had the notion of Odd and Even Numbers, Triangular Numbers, Perfect Numbers, etc. In particular, he is well known today for his Pythagoras Theorem. Although this theorem is known to the Babylonians and Chinese long before Pythagoras, he seemed to be the first person to provide a proof of it.

Zeno of Elea (490-425 BC) is a Greek philosopher famous for his Zeno Paradoxes. He wrote a book containing 40 paradoxes which are concerned with the continuum. Aristotle reproduced 4 of Zeno's paradoxes, The Dichotomy, The Achilles, The Arrow, and The Stadium in his work Physics.
1. The Dichotomy: Before traversing a unit distance we must get to the middle, but before getting to the middle we must get ¹/₄ of the way, but before we get ¹/₄ of the way we must reach ¹/₈ of the way etc. Hence we will never get started!
2. The Achilles: In a race in which the tortoise has a head start, the swifter-running Achilles can never overtake the tortoise because before he comes up to the point at which the tortoise started, the tortoise will have got a little further, and so on ad infinitum.
3. The Arrow: Consider a flying arrow. At any given moment it is in a space equal to its own length, and therefore is at rest at that moment. So, it's at rest at all moments.
4. The Stadium: Consider two chains of atoms (A and C) passing each other, with the chain B fixed:

           A1 A2 A3 =>                                A1 A2 A3
              B1 B2 B3                                B1 B2 B3
              <= C1 C2 C3                             C1 C2 C3
             Instance 1                              Instance 2

The problem with these paradoxes lie in the assumption made by Zeno. Zeno had no concept of non-denumerable sets; he did not know that there are actually different types of infinities; he did not know that the number of points on the integer line is different from the number of points on the real number line. This fact was brought to light by Georg Cantor in the 19^th century. But before they were fully resolved, they stimulated much thought about the foundation of human comprehension and allowed us to understand our world more than before.

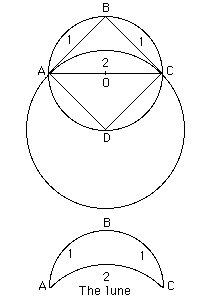Hippocrates of Chios (470-410 BC) is famous for his quadrature of lunes (crescent-shaped figures which are defined by two semi-circles of different radius). He discovered this while trying to 'square the circle'. He also contributed to developments on the problem of 'doubling the cube', as subsequent work on this problem rely on his mean proportionals problem. He showed that a cube can be doubled if two mean proportionals can be determined between a number and its double. The problems of squaring the circle and doubling the cube, together with the problem of trisecting an angle, are the 3 classical impossibility problems (problems without a solution) in Geometry. He provided geometrical solutions to Quadratic Equations and probably knew of the Method of Exhaustion. He wrote Elements of Geometry and it is believed that the content of Books I and II of Euclid's Elements is based on this. His work on the quadrature of lunes relied on his following theorem: AO2 = area of circle with centre O AD2 area of circle with centre D

Theodorus of Cyrene (465-398 BC) was the tutor of Plato and Theaetetus. He is remembered for his contribution to Irrational Numbers. He showed that except for n = 4, 9 and 16, √n is irrational for n between 3 and 17 inclusive (the case for n = 2 was well-known before him). Theaetetus generalized his tutor's work on Irrational Numbers. His main contribution to Mathematics is reproduced in Books X and XIII of Euclid's Elements. The Pythagoreans are attributed with 3 of the 5 Platonic Objects, namely the Tetrahedron, the Cube and the Dodecahedron (the other 2, Octahedron and Icosahedron, are due to Theaetetus).

Plato (427-347 BC) is a philosopher. His contribution to Mathematics is not in discovering new theorems, but rather his idea of mathematical rigor. He concentrated on the idea of 'proof' and insisted on clear definitions and hypotheses. This was to lead to Euclid's systematic approach to Mathematics. Although the Platonic Objects were not discovered by him, they bear his name because he had the idea that the elements (earth, fire, air, and water) together with the universe can be corresponds to each of the 5 Platonic Objects. He had a geocentric idea of the universe (sun and moon revolve round the earth), which we now know is wrong. Although some of his ideas are totally wrong, many others are right. His Plato Academy is the longest surviving institute of learning known.

Hippias of Elias (460-400 BC) is remembered for his Quadritrix. This is a curve with the Polar Equation

πρ = 2rθ csc θ,

which he used to trisect angles and square the circle. Note that this does not contradict the above statement about the impossibility of these problems, because the rule for these classical problems is that they should only be solved via compass and straight edge construction. Later, Archytas of Tarentum (428-350 BC) used the curve to duplicate the cube. Archytas produced a piece of work on the theory of sound. He proved that the product of two consecutive integers do not form a Square Number. This result and the theorems used in its proof would later appear in Book VII of Elements. It is believed that some of the content of Book VII were based on these theorems, which were proved before Archytas; and many of the results in Book VIII were attributed to Archytas.

Eudoxus of Cnidus(408-355 BC) is another prominent figure. His works include Mirror and Phaenomena, as well as others which are lost. His Theory of Proportion enabled people to compared the Irrational to the Rationals (before Eudoxus, these are treated as different objects); and it formed the basis for Book V of the Elements. Although ideas similar to the Method of Exhaustion was known before him, he is the one responsible for formulating this early method of Integration. He used it to prove the following formula:

This method is later extensively used by Archimedes to derived areas and volumes of other objects. In his book On velocities, he discussed his planetary theory, in which he came up with a complex system of 27 spheres to explain planetary motion. Although it is not correct, the system of sphere is consider a great geometrical achievement by many.

Another prominent Greek is Aristotle (384-322 BC). He is a member of the Plato Academy and he is both a philosopher and a scientist. He is said to have worked on Astronomy, Zoology, Psychology, Geography, Chemistry, etc. His contribution to Mathematics is mainly in Logic. Whereas Plato believed that the whole of knowledge can be axiomatized by a single axiom system, Aristotle is more realistic: he believed in multiple axiom systems, each for a different branch of science. In Prior Analytics, Aristotle proposed the now familiar Aristotelian Syllogistic, which is a form of argument consisting of two premises and a conclusion. His example is: If every Greek is a person and every person is mortal, then every Greek is mortal.

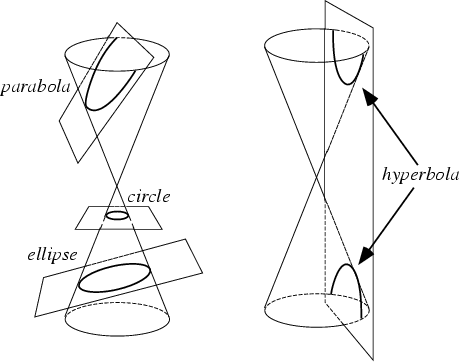Menaechmus (380-320 BC) is remembered for discovering the conic sections, namely that ellipses, parabolas, and hyperbolas are obtained by cutting a cone by a plane. He made this discovery while trying to duplicate the cube by solving the means proportional problem. Subsequently, he duplicated the cube using these conic sections. Suppose given a, b and we want to find two mean proportionals x, y between them. Then a/x = x/y = y/b. From a/x = x/y and a/x = y/b, we have x2 = ay and xy = ab respectively. Solving for x and y is equivalent to finding the intersection of the parabola x2 = ay and the rectangular hyperbola xy = ab. Of course, this is not the way Menaechmus solved the problem; he did not have the convenient tool of Algebra.

Another way to see it is: a/x = x/y � x² = ay, and x/y = y/b � y² = bx. So the solution is given by the intersection of the two parabolas x² = ay and y² = bx. We owe this interpretation to Eutocius of Ascalon (480-540 AD), who wrote this in his commentary to Archimedes' On the Sphere and Cylinder. Again, Eutocius did not do it this way.

Callippus of Cyzicus (370-310 BC) made accurate determinations of the lengths of the seasons and constructed a 76 year cycle comprising 940 months to harmonize the solar and lunar years which was adopted in 330 BC and used by all later astronomers. This formulation resulted in the more accurate 365.25-day tropical year. He also modified Eudoxus 27-sphere system by including 7 more spheres. One of the most prominent mathematician of antiquity is Euclid. Although remembered for his 13 volumes of Elements, he is also the author of many other works. On the Sizes and Distances of the Sun and Moon was written by Aristarchus of Samos (310-230 BC), who tried to determine the sizes and distances of the sun and the moon. Although his estimates were an order of magnitude too small, his line of reasoning was correct, the inaccuracy came from the equipment used. The greatest mathematician of antiquity is Archimedes. He is famed for his works on buoyancy, lever, centre of gravity, volume of sphere, approximation to π, among others. Nicomedes (280-210 BC) is known for his conchoid, which is a curve given by the following Polar Equation

r = b + a secθ

He used this curve to trisect the angle and duplicate the cube.

Chrysippus of Soli (280-206 BC) was the first to organize propositional logic. He produced 118 works on logic and among these, some dealt with the Liar Paradox. This famous paradox results from analysis of the statement

Suppose I'm a truthteller, then this statement would mean I'm a liar; a contradiction. Suppose I'm a liar, then this statement would mean I'm a truthteller, which again is a contradiction. This paradox can take many forms and would lead to G�del's Theorems in 1931.

Eratosthenes of Cyrene (276-194) is famous for the Sieve of Eratosthenes for finding prime numbers. His treatise On the Measurement of the Earth reported an accurate estimate of the circumference of the Earth. Apollonius of Perga (262-190 BC) is also known as the "Great Geometer". His most famous works are the 8 books of Conics. The first 4 books contain results known since Euclid, as well as, some new theorems. The next 4, on the other hand, are highly original. Other works include his famous Apollonius circle (a circle that is tangential to 3 objects, which could be points, lines or circles). Dionysodorus of Caunus (250-190 BC) solved the cubic equation using the intersection of a parabola and a hyperbola; and in On the Tore, he showed the

Zenodorus (200-140 BC) worked on various geometric optimization problems. He showed that the regular n-gon (n-sided polygon) has the greatest area of any n-gon of the same perimeter; that a circle covers the largest area compared to any regular polygon of the same perimeter; that the sphere contains the largest volume compared to any solid figure of the same surface area.

Hipparchus of Rhodes (190-120 BC) produced a table of chords, somewhat like the modern trigonometric tables. He also introduced the division of a circle into 360 degrees.

Geminus (10 BC-60 AD) proved that the helix, the circle and the straight line are the only curves such that any part of the curve is congruent with any other part of the same length. Heron of Alexandria (10-75 AD) is well-known for his formula for the area of a triangle:

where semi-perimeter, s = (a+b+c)/2 and a, b, c are the sides of the triangle. Beside being well-versed in Geometry, he was also a great mechanical engineer, producing many practical and theoretical works in Mechanics. Menelaus of Alexandria (70-130 AD) is the first to treat spherical triangles, i.e. triangles in Spherical Geometry. He proved theorems of spherical triangles corresponding to those in Euclidean Geometry.

Claudius Ptolemy (85-165 AD) is the author of the famous Almagest, which advocates an earth-centred universe. Almagest is somewhat like Euclid's Elements; both consisted of 13 books; Almagest is a collection of ideas in Astronomy till Ptolemy's time, whereas Elements is a collection of ideas in Geometry till Euclid's time. Ptolemy obtained the approximation π = 3 17/120 = 3.14167 using an inscribed 360-gon and √3 = Chord 60o = 1.73205. The Chord function is related to the sine function by sin x = (Chord (2x))/120. With this Chord function, he also deduced the double-angle formula.

Diophantus of Alexandria (200-284) is called the 'Father of Algebra'. His famous work Arithmatica consisted of 13 books containing numerical solutions to algebraic equations. During his time, there was no notion of Zero as a number and Negative Numbers, and the idea of Irrational Numbers had not been fully accepted yet. He only accepted Positive Rational Number solutions, others he rejected as meaningless. He solved algebraically Linear and Quadratic Equations, as well as Simultaneous Linear and Quadratic Equations. He also considered problems such as finding an x such that certain Polynomial Equations in x are Squares or Cubes. E.g. for x = 3/2, he found that 4x + 2 is a cube and 2x + 1 is a square. It is clear that Diophantus may be aware of some very interesting theorems in Number Theory, like Every Rational Number can be written as the sum of four Squares.

However, he would not have been able to prove these, because of a lack of the essential tools for generalizing the problems. E.g. we would write (18 + 9n)/(n³ - 6), whereas Diophantus had to express in words: a ninefold number increased by eighteen, which is divided by the difference by which the cube of the number exceeds six.

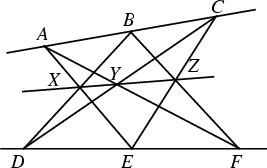
Pappus of Alexandria (290-350) is the author of the work Synagoge (Mathematical Collection), which contains as the name suggests a collection of all the Mathematics known until Pappus' time. Although there is little originality, Pappus showed great understanding in all topics. Book I and II covered Arithmetics. Book III contained a range of topics: mean proportional; arithmetic, geometric and harmonic means; some geometrical paradoxes; inscription of the 5 Regular Polyhedra in a Sphere. Book IV treated curves such as spirals and the quadratrix. Book V reviewed the plane tessellation problem; the 13 semi-regular solids of Archimedes; and the results of Zenodorus. Book VI is on Astronomy and Book VIII is on Mechanics. Book VII contained 'Pappus Problem' (now known as Pappus' Hexagon Theorem). Suppose ABC and DEF are straight lines; and X, Y, Z are the intersections of AE with BD, AF with CD, BF with CE respectively. Then XYZ is a straight line.

Return to Maths Homepage