
| He is considered the greatest mathematician of ancient times. He performed numerous geometric proofs using the rigorous geometry of Euclid. His Method of Exhaustion allowed him to compute areas and volumes of geometric figures. He discovered that the volume of a sphere is 2/3 the volume of the smallest cylinder that can contain it. At his request, the figure of a sphere and a cylinder was engraved on his tombstone. By a series of inscriptions and circumscriptions of regular polygons on a circle, he was able to constrain the value of π between 310/71 and 31/7. |
 |
Archimedes was also a great engineer. He formulated Archimedes' Principle of Buoyancy and the Law of the Lever. The Principle of Buoyancy states that the force exerted on an immersed object (i.e. the buoyancy force) is equal to the weight of the liquid displaced. There is a story regarding Archimedes' discovery of this principle: upon discovering the principle while taking a bath, he jumped out of his bath and ran naked through the streets shouting "Eureka!" (i.e. I have found it!). During the Roman siege of Syracuse, he is said to have single-handedly defended the city by constructing lenses to focus the sun's light on Roman ships and huge cranes to turn them upside down.
Some of his works are Floating Bodies, On Balances and Levers, On Plane Equilibriums, The Sand Reckoner, Quadrature of the Parabola, On Conoids and Spheroids, Measurement of a Circle, On Spirals, and On the Sphere and Cylinder. In 1906, The Methods was discovered. It provides a remarkable insight into how Archimedes discovered many of his results. In On Plane Equilibriums, he found the centre of gravity of parallelograms, triangles, trapeziums and segments of a parabola. Some of his works are discussed below.
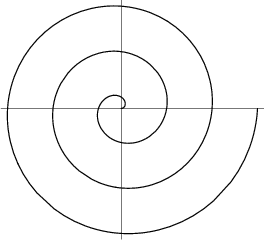
The above graph is that of the Archimedes Spiral. It was studied by Archimedes in On Spirals about 225 BC. The polar equation of the spiral is given as
r = aθ
Archimedes was the first to derive the surface area (S) and volume (V) of a sphere in On the Sphere and Cylinder (ca. 225 BC).
S = 4πr2 & V = 4/3πr3
where r is the radius of the sphere.
The Sand Reckoner is not in itself a theorem or a formula but is more of a show of man's ability to conjure up larger and larger numbers. Archimedes said that:" I will try to show you that some of the numbers I name exceed the number of grains of sand in the universe." In present time, we do not think of this as something very interesting as we can easily write down very large numbers using our decimal number system. But during Archimedes' time, they wrote numbers in words. He assumed there are 10,000 = 104 grains of sand in a poppy seed and a row of 40 seeds is a finger-width. Hence a sphere with a finger-width diameter has (40)3�104 = 64�107. Round 64 to 100, this becomes 109. Now, 104 finger-widths is a stade (approx. 0.1 mile), so there are (104)3�109 = 1021 grains of sand in a sphere with a stade diameter. From Aristarchus's work, he estimated the diameter of the universe based on the following formula he assumed:
| diameter of earth | = | diameter of S |
| diameter of S | diameter of universe |
where S is a sphere with diameter from earth to sun. From Aristarchus' figures, he obtained 1014 stadia for the diameter of the universe. Hence, the universe can be filled with (1014)3�1021 = 1063 grains of sand. Archimedes denoted 10,000 as a myriad and a myriad myriad as 108. Then he said any number up to a myriad myriad is a number of the first order, any from 108 to 1016 is of the second order, and so on until (108)99,999,999 to (108)100,000,000 is of the 108 order. He then called any number up to the 108 order a number of the first period. Repeating the process for the order on the period, he got finally to the myriad-myriad units of the myriad-myriadth order of the myriad-myriadth period which is our 1080,000,000,000,000,000.
Return to Maths Homepage