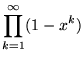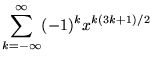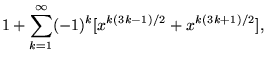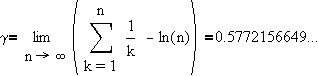Euler

The Mathematics of Leonhard Euler (1707 - 1783) (Swiss)

Leonhard Euler (pronounced 'oiler') of Basel, Switzerland, is an extraordinary mathematician. He alone has produced more works than any other mathematicians. All of these works are of extremely high quality, and he produced the most ingenious and beautiful proofs ever. Even until now, his works are still under compilation and revision. He is truly a mathematical genius. He lost the sight in the right eye at about 30 and then both in his early 60s. Even when he has gone totally blind, he was still constantly producing great works. He would work through highly complicated calculations and derivations in his mind, and recite the statements one-by-one to his daughter, who does the writing for him. His memory has to be extraordinary to do this. He was productive till the end. He has contributed to almost all fields of Mathematics and he is also the founder of other fields, e.g. Topology. He introduced the world to many of the mathematical symbols used by us today. Among these are e, the base of natural logarithm, and i, the square root of -1. He published the first great textbook on analysis in 1748 Introductio in analysin infinitorum (Introduction to the Analysis of the Infinites).

Euler was a friend of Daniel Bernoulli. When Daniel's brother, Nicholas Bernoulli, died in 1726, Daniel recommended Euler for the post at the St Peterburg Academy (founded 1725) in Russia. Euler took it up in 1727. When Daniel left for Basel in 1733, Euler assume the chair of Mathematics. He worked there for 13 years. Then in 1741, he was invited to be the director of Mathematics at the Academy of Science in Berlin and he stayed there for 25 years. After that, he returned to Russia to resume his position, which was still open for him! He stayed there for the rest of his life.

Here's a sample of his great many works.

1. Pentagonal Number Theorem

Pentagonal numbers are numbers of the form n(3n-1)/2, where n is a natural number. The generalized pentagonal numbers are of the same form, but with n as integers. It is easy to show that the generalized pentagonal number is of form n(3n-1)/2 or n(3n+1)/2. Euler proved that,

	=
	=

2. Euler Identity

The interesting identity,

was proved by Euler, while trying to solve Bachet's Conjecture, which states that every positive integer can be written as the sum of at most four squares. Bachet's Conjecture is a special case of Fermat's Polygonal Number Theorem.

3. Euler Polyhedral Formula

Consider a simply-connected polyhedron of V number of vertices, F number of faces and E number of edges. Euler proved that,

V + F - E = 2

This is later generalized by Poincare to

V + F - E = 2-2g,

for a surface of genus g. The genus of a surface is the number of holes in the surface.

4. Euler Formula

Euler proved the following formula,

cosx + isinx = e^ix

and deduced the beautiful and extraordinary formula that links the 5 fundamental constants in Mathematics, namely, e, i, π, 1 and 0, together.

_eiπ _{+ 1 = 0}

5. Graph Theory

Euler's solution to the K�nigsberg Bridge problem (a Graph Theory problem) marks him as the founder of Topology. The graph is shown below. The aim is to traverse the graph with a pencil without lifting the pencil or retracing the lines. You'll find that this can't be done.

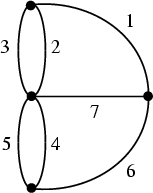
Euler noted that all the nodes have an odd number of edges joined to them. He showed that this is sufficient to prove the impossibility of traversing the graph. The word 'topology' was coined by Johann Listing in 1836. Listing wrote a book Preliminary Sketch of Topology in 1847.

Other accomplishments

i. Every prime of the form 6n+1 can be written in the form x²+3y².

ii. Euler modified formula

iii. Euler-Mascheroni constant

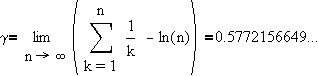
iv. Basel Problem

v. Euler Product Formula

vi. Euler-Maclaurin series

Short notes on some of the mathematicians mentioned in this page.
1) Bachet () ()

2) Johann Listing () () was a professor of mathematical physics at G�ttingen University. He independently discovered the M�bius strip in 1858 (same year as M�bius).

3) Mascheroni () ()

4) Colin Maclaurin () (Scottish) worked independently of Euler in 1740.

Return to Maths Homepage