The Story of Number Theory (NT) is essentially a story of prime numbers. Natural Numbers are the counting numbers 1, 2, 3, 4 ... and is collectively known as N. The factors of a natural number n are the natural numbers which divide n evenly. For every n, 1 and n are always factors, the other factors are called proper factors. Prime Numbers are natural numbers which have no proper factor. E.g. 5 is a prime because its only factors are 1 and 5; 6 is not prime because 1, 2, 3, 6 are all factors. Number Theory is not restricted to natural numbers only. In fact, it involves not only rational numbers, but also real numbers and in general complex numbers. Rational Numbers Q are formed by dividing one natural number by another, i.e. they are fractions. E.g. 5/6, 2130/7369, 4/1. Hence all natural numbers are rational numbers. When expressed in their decimal notation, they either have a finite decimal representation or they have recurring digits. E.g. 80/99 = 0.808080... and 3/625 = 0.0048. Irrational Numbers are those which can't be expressed in this form. They include numbers like √2, p and e. p is the ratio of a circle's circumference to its diameter, 3.14159...; and e is the base of natural logarithm, 2.71828... The rationals and the irrationals together form the Real Numbers R. The Complex Numbers C are numbers of the form a+bi, where a and b are real numbers and i = √-1. There is another classification of the Reals, namely into Algebraic A and Transcendental Numbers. The former are those which can be obtained by solving polynomial equations with integer coefficients. The latter are those that cannot. Hence, all rationals are algebraic since x = b/a is the solution to the equation ax - b = 0, where a and b are integers. Irrationals may or may not be algebraic, e.g. both e and π are transcendental. The proofs of which were due to Hermite in 1873 and Lindemann in 1882 respectively.
Back to the primes. The sequence of primes is as follows: 2, 3, 5, 7, 11, 13, 17, 19, 23, ... There appear to be no particular order involved except that other than the first, all are odd. Is it possible to tell in advance what is the nth prime? Are there infinitely many primes? Why are they so important?
The Prime Factorization Theorem tells us that every natural number can be expressed uniquely as a product of primes.
Eratosthenes devised an algorithm to methodologically find the primes. This algorithm is called the Sieve of Eratosthenes. Write the first n natural numbers in a table. First of all, strike out the number 1. The smallest number in the table is now 2. Strike out all the multiples of 2 except 2 itself. The next smallest number left is 3. Strike out multiples of 3 except 3 itself. The next smallest number left is 5. Strike out all multiples of 5 except 5 itself. Continue doing this, identifying the next smallest number p and striking out multiples of p except p itself. Notice I've used the letter p, because all the 'smallest number left' are prime. The remaining numbers in the table are all primes, which I've highlighted in red for clarity. The algorithm can be stopped when p is ≤ √n.
| 2 | 3 | 5 | 7 | ||||||
| 11 | 13 | 17 | 19 | ||||||
| 23 | 29 | ||||||||
| 31 | 37 | ||||||||
| 41 | 43 | 47 | |||||||
| 53 | 59 | ||||||||
| 61 | 67 | ||||||||
| 71 | 73 | 79 | |||||||
| 83 | 89 | ||||||||
| 97 |
From the table, it looks like the primes are thinning out. This raises the question "Is the sequence of primes finite?" Euclid proved that there are infinitely many primes. His proof is the first and most elegant one. Suppose there are a finite number of primes of which the biggest is N. Let's form the number M = 1�2�3�...�N + 1. Since none of the N primes divide M, either M has a smallest proper factor greater than N or it has no proper factors. In the former, there is a smallest proper factor greater than N and it has to be prime otherwise it would have a smaller factor, contradicting it being the smallest. In the latter, M is prime, thus there is a prime greater than N, a contradiction.
Another thing you can observe from the table is the primes seem to be random. Is it possible to know the nth prime in advance without going through the tedious sieve? There are bulky prime-generating formulae, but all are hard to use. However, in this apparent randomness there is order, as we know from the Prime Number Theorem.
The Prime Number Theorem (PNT) states that the number of primes less than n, denoted by π(n), is n / ln n for large n.
![]()
Gauss was the first to discover this in 1792. But Legendre was the first to publish it in 1798 (independently). The notation π(n) is due to Landau in 1909. Note that the PNT is equivalent to the following statements:
i) The probability of n being a prime is ~ 1 / ln n. (This one can be obtained from PNT by dividing both sides by n.)
ii) The nth prime is ~ n � ln n. (This one can be obtained by observing that on average the nth prime pn = n�a/b, where b is the number of primes from 1 to a. From PNT, b ~ a / ln a, hence pn = n ln a. But for large n, n ~ a, thus pn = n ln n.)
Consider the table below with the third column round off to the nearest natural number.
| n | π(n) | n/ln n |
| 103 | 168 | 145 |
| 106 | 78,498 | 72,382 |
| 109 | 50,847,534 | 48,254,942 |
| 1012 | 37,607,912,018 | 36,191,206,825 |
| 1015 | 29,844,570,422,669 | 28,952,965,460,216 |
| 1018 | 24,739,954,287,740,860 | 24,127,471,216,847,323 |
As n gets larger, it becomes more accurate. Besides the apparent randomness and thinning out of the primes, there's also the spreading and clustering of the primes. An unsolved problem in NT is if there are infinitely many twin primes. This is known as Goldbach's Twin Prime Conjecture. If this is true, then we have the most obvious case of prime clustering. Goldbach has many prime number conjectures to his name. Another is his 1742 conjecture, which states that every even integer >2 is expressible as the sum of two primes. Estermann proved, in1929, that this is almost always true.
Subsequently, PNT has been refined by the Logarithmic Integral,
Li(x) =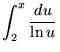
This is because for large x, Li(x) ~ x/ln x. Hence from the PNT
π(x) ~ Li(x)
This is a much better approximation for π(n). This is often called the Improved PNT. A good approximation of Li(n) is 1/ln 2 + 1/ln 3 + 1/ln 4 + ... + 1/ln n.
Chebyshev wrote 2 papers on PNT. His 1849 paper showed that if π(n) ~ Cn/ln n for some fixed number C, then C = 1. His 1850 paper showed 2 things. The first is Bertrand's 1845 postulate which states that between any number and its double, there is always a prime. The second is that 0.9n/ln n < π(n) < 1.1n/ln n. Both results in the second paper was obtained by converting Stirling's formula (for large n, n! ~ nn e-n √2πn) into one having a step function and proving through elementary methods. Another of Chebyshev's contribution to NT is the Chebyshev bias. Consider dividing an odd prime by 4, the remainder is either 1 or 3. For p=101, the ratio of reminder1 to remainder3 is 12:13, a bias towards 3. For p=10,007, the ratio is 609:620, again a bias towards 3. In fact, this bias is not violated until p=26,861. When the divisor is 3, the remainders are either 1 or 2, and the bias here is greater. The first violation occurs at p=608,981,813,029.
In 1884, Sylvester improved Chebyshev's
limits to 4%. In 1895, von Mangoldt proved the main result in Riemann's
1859 paper (see below). It was then clear that if a weaker form of the Riemann
Hypothesis (RH) is right, then PNT would be proven. Hadamard and
Poussin independently proved the PNT in 1896 via this path using complex function theory.
In
1949, Selberg proved it via elementary means.
Littlewood proved in 1914 that Li(x) - π(x)
changes from positive to negative and back infinitely many times. A Littlewood
violation is when the difference is negative.
In the same paper, he also proved that the
Chebyshev bias is violated infinitely many times. In 1933, his student Skewes
assuming the RH is true, showed that an upper bound for the
first Littlewood violation is
![]() , a number with 1010
octillion digits. This number is now known as Skewes' number. In 1955,
Skewes improved his result without having to implicate RH and lower the number
to 101000 digits. In 1966, Lehman improved on it to 1.165�101165
(which has 1166 digits) and proved a theorem for the upper bound. Using Lehman's
theorem, Riele reduced it to 6.658�10370. In 2000, Bays and
Hudson improved it further to 1.39822�10316 also
using Lehman's theorem. They also showed a huge zone of violation around
1.617�109608.
, a number with 1010
octillion digits. This number is now known as Skewes' number. In 1955,
Skewes improved his result without having to implicate RH and lower the number
to 101000 digits. In 1966, Lehman improved on it to 1.165�101165
(which has 1166 digits) and proved a theorem for the upper bound. Using Lehman's
theorem, Riele reduced it to 6.658�10370. In 2000, Bays and
Hudson improved it further to 1.39822�10316 also
using Lehman's theorem. They also showed a huge zone of violation around
1.617�109608.
In 1901, von Koch proved that if the RH is true, then
π(x) = Li(x) + O(√xlnx)
The rightmost term is called the big oh function and it first appeared in Bachmann's 1894 treatise, but was made famous by Landau's 1909 book. It is defined as below: Function f is big oh of function g if, for large enough arguments, the size of f never exceeds some fixed multiple of g, i.e. f(x) = O(g(x)) if for large x, |f(x)| < |Kg(x)|, where K is a constant. E.g. 0.1x = O(x) and lnx = O(x), but x2 ≠ O(x). Note that von Koch's result is equivalent to |π(x) - Li(x)| < K√x lnx, which was what von Koch himself wrote. xlnx is the simplest function known, but it depends on the truth of RH. The simplest that doesn't depend on the truth of RH is
O(xe-C[(lnx)3/5/(ln lnx)1/5])
where C is a constant. Since lnx is eventually smaller than any power of x, lnx = O(xε), where ε is an infinitesimal number. Hence von Koch's result can be re-written as
π(x) = Li(x) + O(x�+ε)
Note that this is a weaker form of von Koch's result. Li-1(n) gives the nth prime correct to about half way along. E.g. the 109th prime is 22,801,763,489, whereas Li-1(109) = 22,801,627,415.
The harmonic series is a series of great interest for many reasons. It's the sum of the reciprocal of all the natural numbers.
1 + 1/2 + 1/3 + 1/4 + ...
The simplest and most elegant proof of the divergence of the harmonic series was obtained by Oresme (1323-1382). Observe that 1/3 + 1/4 > 1/2, 1/5 + 1/6 + 1/7 + 1/8 > 1/2 and so on, then adding up the series is like adding up infinitely many terms each greater than 1/2, hence the sum is infinite. Like many works of early mathematicians, their works remain unknown to most of the other mathematicians. So in 1647, Mengoli proved its divergence with another method. Later on, Johann and Jacob Bernoulli each produced their own proofs.
Mengoli posed the Basel Problem, which asked for a closed form solution to
1 + 1/22 + 1/32 + 1/42 + ...
It was solved in 1735 by Euler, who in fact solved a greater problem: the closed form solution for all even powers. The harmonic series and the Basel Problem can be generalized to the Riemann zeta function
ζ(s) = 1 + 1/2s + 1/3s + 1/4s + ...
Euler worked out by hand the cases s = 2 to 26, giving ζ(2) = π2/6, ζ(4) = π4/90, ζ(6) = π6/945, ..., ζ(26) = 1315862π26/11094481976030578125. This is an extraordinary achievement considering there was no computer back then! The case for the odd powers (>1) remained unsolved. In 1978, Ap�ry proved that ζ(3) is irrational. ζ(3) is hence known as Ap�ry's number. An application of this number is as follows: select 3 natural number at random, what is the chance they have no common proper factor? Answer is 1/ζ(3).
In 1737, Euler made another progress on the zeta function. In his book Various Observations about Infinite Series, he proved the Euler Product Formula.
Dirichlet proved in 1837 that each infinite Arithmetic Progression (AP) with first term and common difference without a common factor, contains infinitely many primes. Consider the first term 4 and common difference 5, the AP is 4, 9, 14, 19, 24, 29, ... The first few primes are 19, 29, ... and Dirichlet guaranteed that there are infinitely more to come. He proved this using Euler Product Formula and Gauss' Arithmetic of Congruence. Consider all the numbers < n which do not have a common factor with n. Let these numbers be a1 to am, and generate the m APs with first term ai, i = 1 to m, and common difference n. A more general theorem states that these m sequences have the same proportion of primes. E.g. n = 6, then the a's are 1 and 5, and the 2 sequences are
1, 7, 13, 19, 25, 31, 37, 43, 49, 55, 61, 67, 73, 79, 85, 91, 97, ...
5, 11, 17, 23, 29, 35, 41, 47, 53, 59, 65, 71, 77, 83, 89, 95, ...
There are 11 primes in the first and 12 in the second, about the same in each sequence. It gets more accurate with more terms.
One of the biggest names in Analytic NT is the German mathematician Georg Friedrich Bernhard Riemann (1826-1866). Riemann came from a poor family and was frequently sick and homesick. He entered the University of G�ttingen (founded 1734) in 1846. G�ttingen was the hometown of Gauss, who was Riemann's greatest idol. In 1851, he got his doctorate, which was on complex function theory. In his habilitation thesis, he presented the Riemann integral. In his 1854 habilitation lecture, he presented the geometry (the theory of Riemann surfaces) which Einstein would eventually adopt for his General Theory of Relativity. In 1857, he published an important paper on Analysis Theory of Abelian Functions. Soon his name was well-known throughout the mathematical community in Europe. Based on the 1851 and 1857 papers, he was appointed a member of the Berlin Academy in 1859. As such he had to present an original paper to the Academy, which he did and this paper will forever change the future of Number Theory. The title of this paper was On the Number of Prime Numbers Less Than a Given Quantity and it gave the now famous Riemann Hypothesis. With Fermat's Last Theorem solved, this is now the greatest unsolved problem in NT.
Riemann Hypothesis states that ζ(a+bi) = 0, where b ≠ 0 � a = 1/2, i.e. all non-trivial zeros of ζ(s) have real part 1/2. The notation ζ(s) is due to Riemann. The weaker form that was mentioned above is that all non-trivial zeros of ζ(s) have real part < 1.
Some facts about the non-trivial zeros are:
1. There is an infinity of them, all having real parts between 0 and 1. This is known as the critical strip (in complex number notation 0 < Re(z) < 1). RH says that they all lie on the critical line (Re(z) = 1/2).
2. They occur as conjugate pairs, i.e. if z = a+bi is a zero, then z = a-bi is as well.
3. Their real parts are symmetrical about the critical line, i.e. a zero is either on the critical line or if (1/2+α) + it is a zero, so is (1/2-α) + it.
Using Euler-Maclaurin series, J�rgen Gram calculated the first 15 zeros in 1903 and the list starts 1/2 + 14.1347...i, 1/2 + 21.0220...i, ... Riemann had suggested a formula for the number of zeros with imaginary part between 0 and some large T (actually he didn't include the error term O(lnT), this was added in later).
N(T) = (T/2π) ln(T/2π) - T/2π + O(lnT)
This was proven in 1905 by von Mangoldt. Remember from the definition of big oh, that O(lnT) is less than a certain multiple of lnT. This multiple turn out to be less that 0.14. Hardy proved in 1914 that there are infinitely many non-trivial zeros on the critical line. There are theories that allow us to calculate the number of zeros in the critical strip within the interval T1 and T2, as well as the number of zeros on the critical line within the same interval. If these 2 numbers are not equal for some interval, then RH is false. Siegel published the Riemann-Siegel formula in 1932 after examining Riemann's papers deposited in the G�ttingen archive. With this formula and the advent of computer, computations of the zeros has become easier. Using these theories, the number of zeros less than 1011 has been computed and all were found to be apparently irrational numbers (all numbers computed are accurate to a certain decimal point only). It is still unknown if a rational zero exists. The average spacing of zeros in the critical strip at height T is 2π / ln(T / 2π).
In 1921, Artin developed an algebraic approach to RH via Field Theory. He extended a finite field to associate this extension with a zeta function. This field has its own zeta function, Euler product and RH. In 1933, Hasse proved a result analogous to RH for a certain category of those base fields. In 1942, Weil (pronounced 'Vay') extended this proof to a much wider class of objects and similar results would apply to yet wider classes in his 2 Weil Conjectures. In 1973, Deligne prove these conjectures. The field associated with RH is the rational numbers. It is not known if all these results will help in solving the RH yet, but it has allowed Wiles to prove Fermat's Last Theorem.
Yet another approach is through Matrix Theory. A Hermitian matrix is one in which the number at row m column n is a+bi and that in row n column m is a-bi. This applies to all terms in the matrix, including the diagonal, hence the diagonal terms must be real numbers since a+bi = a-bi � b = -b � b = 0. The eigenvalues of a Hermitian matrix was real too, so are the coefficients of the characteristic polynomial. The Hilbert-P�lya Conjecture says that the non-trivial zeros of the Riemann zeta function corresponds to the eigenvalues of some Hermitian matrix. Hilbert and P�lya worked independently. In 1973, Montgomery assuming the truth of RH, proved a theorem regarding the statistically properties of the spacing between non-trivial zeros of the zeta function. He also gave the Montgomery pair-correlation conjecture, which says that the distribution function of those spacings had an integrand 1 - (sinπu/πu)2 and is same as the form factor for the pair correlation of eigenvalues of Gaussian-random Hermitian matrices. The latter had been pointed out to him by the physicist Freeman Dyson, who works with these matrices in quantum mechanics. By Gaussian-random, it means the random number generator is from a Gaussian distribution, i.e. most of the numbers picked for the Hermitian matrices are close to the centre of the Gaussian distribution. The set of these matrices is called the Gaussian Unitary Ensemble, GUE. The property of the eigenvalues of the Gaussian random numbers is that when line up on a real number line, the points seem to repel each other, meaning there is no clustering on the number line. The same is true for the t values of the non-trivial zeros �+it. Truly random numbers will have some clustering here and there. In 1987, Andrew Odlyzko computed various non-trivial zeros and checked their spacing against those of the eigenvalues of GUE matrices. From his results, he published a paper On the Distribution of Spacings Between Zeros of the Zeta Function. The main result of the paper is now called the Montgomery-Odlyzko Law: The distribution of the spacings between successive non-trivial zeros of the Riemann zeta function (suitably normalized) is statistically identical with the distribution of eigenvalue spacings in a GUE matrix. Note that this is a law and not a theorem, it just states what is observed and hence is physical rather than mathematical.
The M�bius function μ(n) where n is a natural number is defined as below:
1. μ(1) = 1
2. μ(n) = 0 if n has a square factor
3. μ(n) = -1 if n is a prime or the product of odd number of distinct primes
4. μ(n) = 1 if n is the product of even number of distinct primes
With this function the reciprocal of ζ(s) can be written as 1/ζ(s) = ∑ μ(n) / ns. See here.
Mertens' function is defined as M(k) = μ(1) + μ(2) + μ(3) + ... + μ(k). If M(k) = O(k�), then RH follows, hence this is a stronger statement then RH. Modifying this into M(k) = O(k�+ε), we get a statement equivalent to RH.
Consider the function
J(x) = π(x) + 1/2 π(√x) + 1/3 π(3√x) + 1/4 π(4√x) + ...
Note that for any x, there is nth root beyond which π(m√x) = 0 for m>n. E.g.
J(20) = π(20) + 1/2 π(4.47...) + 1/3 π(2.71...) + 1/4 π(2.11...) + 0 + ... = 8 + 1/2 (2) + 1/3 (1) + 1/4 (1) = 9.5833...
By M�bius inversion, we can express π(x) in terms of J(x)
π(x) = J(x) - 1/2 J(√x) - 1/3 J(3√x) - 1/5 J(5√x) + 1/6 J(6√x) ... = ∑[μ(n)/n � J(n√x)]
n
By taking logarithm of the zeta function (product form in the Euler Product Formula), applying the infinite series of ln (1-x), and regrouping the terms, we get
∞
1/s ln ζ(s) = ∫J(x)x-s-1dx
0
If you invert this, you get
∞
J(x) = Li(x) - ∑Li(xρ) - ln2 + ∫1/[t(t2-1)lnt]dt
ρ 0
where ρ are all the non-trivial zeros of the zeta function. This is the main result of Riemann's 1859 paper. Since we are only interested in x≥2, the sum of the last 2 terms is always between -0.6931... and -0.5531... And since we are interested in large x, this is negligible compared to the first 2 terms. The first term is just the logarithmic integral. Since the non-trivial zeros occur as conjugate pairs ρ and ρ, and Li(xρ) and Li(xρ) also occur as conjugate pairs, the second term is a real number. Hence, the number of primes less than x is closely related to the non-trivial zeros of the zeta function.
Lindel�f wrote the Lindel�f Hypothesis (LH) in 1908. It is concerned with the value of μ as σ varies in |ζ(σ+it)| = O(tμ). The μ here is the Lindel�f function and O is the big oh function. μ is a function of σ. It is known that |ζ(σ+it)| = O(tμ+ε). But this is not what LH is about. It is known that for σ ≤ 0, μ(σ) = � - σ; for σ ≥ 1, σ = 0; for σ in the critical strip, μ(σ) < �(1 - σ); μ(σ) is convex downward. LH states that μ(�) = 0. If this is true, then it implies that for σ ≤ �, μ(σ) = � - σ; and for σ > �, σ = 0. If RH is true, then LH follows.
Short notes on some of the mathematicians mentioned in this page.
1) Ferdinand von Lindemann (1852-1939) (German) proved π is
transcendental using Hermite's result on e.
2) Edmund Landau (1877-1938) (German) came from a wealthy family and became a professor at G�ttingen in 1909. He wrote more than 250 papers and 7 books. His 1909 Handbook of the Theory of the Distribution of the Prime Numbers was the classic on Analytic Number Theory.
3) Theodor Estermann (1902-1991) ()
4) Pafnuty Lvovich Chebyshev () (Russian)
5) Joseph Bertrand () (French)
6) James Stirling () (Scottish) produced Stirling's formula in 1730.
7) J. J. Sylvester () (American) at John Hopkins University in US invented matrices and theory of algebraic invariants with Arthur Cayley.
8) Hans von Mangoldt () (German)
9) Jacques Hadamard (1865-1963) (French) had original work in various fields of Mathematics. He proved the Three Circle Theorem of Complex Function Theory in 1896.
10) Charles de la Vall�e Poussin () (Belgian)
11) Atle Selberg (1917-) (Norwegian) works at the Institute of Advanced Study in Princeton, New Jersey. He had communicated some preliminary ideas with Paul Erd�s who then provided his own elementary proof of the PNT.
12) John Edensor Littlewood (1885-1977) (English)
13) Samuel Skewes () ()
14) Sherman Lehman () ()
15) Herman te Riele () ()
16) Carter Bays () ()
17) Richard Hudson () ()
18) Helge von Koch () (Swedish) is famous for his Koch snowflake curve.
19) Paul Bachmann () () was the first to publish a book on Analytic Number Theory in 1894.
20) Pietro Mengoli () () was a professor at the University of Bologna. He first posed the Basel Problem in 1644.
21) Roger Ap�ry (1917-) (Greek-French)
22) Lejeune Dirichlet (1805-1859) (German) was Riemann's teacher and he contributed much to Analysis. When Gauss died, he took over his position in G�ttingen. When he died of heart attack, his brain was preserved and stored at the University, and Riemann took over his chair.
23) J�rgen Gram () (Danish) was an amateur mathematician who worked as an insurance company executive. He died of a freak accident: struck and killed by a bicycle.
24) Godfrey Harold Hardy (1877-1947) (English)
25) Carl Ludwig Siegel () (German) was a number theorist.
26) Emil Artin () (Austrain)
27) Helmut Hasse () () worked at the University of Marburg in Germany.
28) Andr� Weil () () was Hadamard's student.
29) Pierre Deligne () (Belgian) won the Fields Medal for proving Andr�'s Conjectures.
30) David Hilbert (1862-1942) (German) is famous for his 1900 presentation of 23 of the most daunting Mathematical Problems (Hilbert Problems). He also did many great works. In 1888, he solved Gordon's Problem in the theory of algebraic invariants, which is concerned with the existence of a certain class of objects. He proved that the objects exist. He also created new proofs for the transcendentality of π and e. He took over the G�ttingen chair from 1895-1930.
31) George P�lya (1887-1985) (Hungarian)
32) Hugh Montgomery () (American)
33) Andrew Odlyzko () ()
34) Augustus M�bius (1790-1868) (German) is famous for the M�bius strip (1858). He introduced his M�bius function in 1832.
35) Franz Mertens () () gave us the notation μ(n) in 1874.
36) Ernst Lindel�f (1870-1946) (Finnish) wrote a text of complex function theory Calcul des R�sidus.
Return to Maths Homepage