Pascal

The Mathematics of Blaise Pascal (1623-1662) (French)

Pascal started to work on geometry himself at the age of 12. He rediscovered that the sum of the angles of a triangle are two right angles. At the age of 16, Pascal discovered a number of Projective Geometry theorems, including Pascal's Mystic Hexagon. In 1640, he published his first work, Essay on Conic Sections. He invented the first digital calculator to help his father with his tax-collecting. From 1646 onwards, Pascal began a series of experiments on atmospheric pressure. By 1647 he showed that a vacuum existed. In 1653, he wrote a treatise explaining Pascal's law of pressure. This treatise is the first complete outline of a system of hydrostatics. Pascal was not the first to study the Pascal triangle (and binomial coefficients), but he produced the most important work on this topic and this led Isaac Newton to discover the general binomial theorem for fractional and negative powers. He and Pierre de Fermat are the founders of Probability Theory.

We'll look at some of Pascal's work below.

1. Pascal's Triangle

                   1
                 1   1
               1   2   1
             1   3   3   1
           1   4   6   4   1
         1   5   10  10  5   1
       1   6   15  20  15  6   1
     1   7   21  35  35  21  7   1
   .   .             .         .    .
 .   .               .           .    .

The next row is obtained by adding the adjacent terms of the previous row. These numbers are the coefficients of the Binomial Theorem:

where,

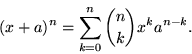
n! (pronounced "n factorial") is the product of the first n natural numbers. E.g. 3! = 6, 4! = 24. He found the Binomial Theorem for positive integer powers. The theorem was later generalized to real powers.

2. Probability Theory

In correspondence with Fermat he laid the foundation for Probability Theory. This correspondence consisted of five letters in 1654. They considered the Dice Problem and the Problem of Points. The Dice Problem asks how many times one must throw a pair of dice before one expects a double six while the Problem of Points asks how to divide the stakes if a game of dice is incomplete.

Problem of Points
The original problem posed to Fermat was: Consider two players, A and B. A needs 2 points to win and B needs 3 points. What is A's chance of winning over B's? Fermat's answer to this is A's 11/16 as to B's 5/16. Pascal generalized this problem to: A needs m points to win, whereas B needs n points to win; and his solution is that A's chance of winning is

sum of first m terms in the (m+n)th row of Pascal's Triangle sum of entire (m+n)th row

and B's chance of winning is the complement of this.

3. Cycloid

His last work was on the cycloid, the curve traced by a point on the circumference of a rolling circle. He applied Cavalieri's calculus of indivisibles to the problem of the area of any segment of the cycloid and the centre of gravity of any segment. He also solved the problems of the volume and surface area of the solid of revolution formed by rotating the cycloid about the x-axis.

The equation of the cycloid with a cusp at the origin is

In parametric form, this is

x = a(t - sint)

y = a(1 - cost)

Return to Maths Homepage