How Mathematics Begin

Counting

Believe it or not, Mathematics started way back in prehistory. The oldest mathematical record is found on a baboon bone (known as the Lebombo Bone) 35,000BC in Swaziland. There were 29 notches on the bone. This is believed to be a record of the lunar cycle. The Paleolithic humans of Europe 30,000BC left evidence of counting on wolf bone. 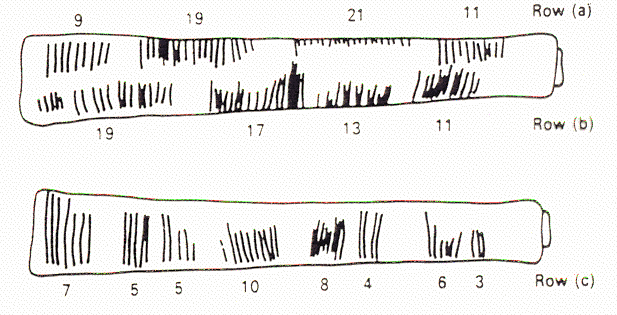And at 23,000BC, the humans of Congo left evidence of markings on the Ishango bone. Yes, Mathematics began with counting. Counting is Mathematics in its most basic form because the basic foundation of Arithmetic is counting. Definitely counting would have started long before 35,000BC. Our ancestors would have carve a stroke on a rock, bone, wood, etc to signify one object or one day passed. This is the simplest way of counting. The next simplest counting method is the one-two-many method in which anything more than two is simply known as many. But in this method, there is no way to tell a person the difference between 3 and 4, both will be known as many. Entered the 2-count system. In this system, to count 3 one simply has to say 2-1; 4 would be 2-2, etc. Some primitive tribes in Africa and South America still use this system. This system is inefficient for counting large numbers so better systems evolved. The 4-count system is an extension of the 2-count system. Then it gets more sophisticated, the Huku tribe of South America uses the 4-12 system that has words for 1, 2, 3, 4 and 12, hence 19 is known as 12-4-3. The Aztec and Mayans used a 5-10-20 system. The Sumerians used a 10-60 system. More on Number Systems here.

More on the Ishango Bone. It is said that the markings signify that there was deeper understanding of numbers. It is said that they were fascinated by prime numbers too: row (b) contains all the 4 primes between 10 and 20. Row (a) is said to be craved based on the knowledge that 10-1, 20-1, 20+1, 10+1 represent some sort of pattern: these are the numbers that differ from 10 and 20 by 1. Row (c) seems to show knowledge of doubling (2�3=6, 2�4=8, 2�5=10), halving (6/3=8/4=10/5=2) and difference of 2 (7-5). Definitely this interpretation is highly controversial, as all these seem too advance for the Paleolithic. Ishango Bone

Geometry

Geometry came in next about 25,000BC with simple geometric shapes. The Paleolithic humans probably are capable of drawing simple geometric shape with a stone or a stick to represent the moon, the sun or anything they see in their everyday life way before the 25,000BC. However, this is not considered Geometry but simply as painting. It can only be treated as Mathematics if there is abstraction or calculation involved. Mathematics could not advance if human remain hunter-gatherers. Around 10,000BC agriculture was invented and with that came the need to keep accounts and maintain farm areas.

Babylonian

The Babylonians lived in Mesopotamia (a part of present day Iraq) from the 4000BC. Technically, the Babylonians really existed from 2000BC from Babylon, which is a part of Mesopotamia. From 4000-2000BC, the area is dominated by Sumerians and then Akkadians. At 4000BC the Sumerians devised a calendar. They built homes and temples and decorated them with artistic pottery and mosaics with geometric patterns. They created a sexigesimal number system mainly for the purpose of keeping track of financial transactions. This system has symbols for 1, 10, 60, 600, 3600 and 36000. They created the cuneiforms by 3400BC. The number system in cuneiforms is place-valued and only has symbols for 1 and 10. However, it does not distinguish 601 from 61 because of the lack of a symbol for zero. They divided a day into 24 hours, an hour into 60 minutes and a minute into 60 seconds. It is credible that this system has survived till now. The Babylonians were capable of solving quadratic equations (1950BC), Pythagoras Theorem is known to them (1850BC) and they used multiplication tables (1800BC). In 1750BC, they solved linear and quadratic equations algebraically, they have tables for square and cube roots, and they applied Mathematics (including Pythagoras Theorem) to astronomy. In practical cases, they took π to be 3, but they have better approximation of π as 3 1/8 according to the tablet that compares the perimeter of hexagon to the circumference of circle.

Egyptian

The Egyptians devised their own calendar at 4000BC. At 3400BC, Egyptian Hieroglyphic numerals took shape.

 

1 10 100 1,000 10,000 100,000 1,000,000

 

They built the Great Pyramid of Giza at 2650BC. However, Hieroglyphic requires many symbols for calculation, so Hieratic was developed. Hieratic has symbols for 1-10, 20, 30, ...,100, 200, ..., 1000, 2000, ..., 9000. The Egyptians made the first mathematical manuscripts in 1900BC: the Moscow Papyrus which contained 25 problems on Geometry. In 1700BC, Ahmes produced the Rhind Papyrus which contained even more problems, altogether 87 on Arithmetic, Algebra and Geometry. Ahmes was a scribe and he mentioned that he copied the Rhind Papyrus from a document 200 years old.

Chinese

The Chinese calendar began around 2953BC and is based on the lunar cycles. It's still in use today. At 2000BC, Yu the emperor is said to have encountered magic squares. The first evidence of Chinese numerals is at 1400BC, where records are found on bones and tortoise shells. It is a decimal place-valued system (with a space to represent zero). The Chinese used counting boards at 1000BC and counting rods at 540BC. Pythagoras Theorem is known to the Chinese before Pythagoras. Most of the history of Chinese Mathematics was destroyed during 213BC when the emperor of unified China of Qin Dynasty ordered all books and scholars to be burnt. The earliest existing manuscript is the Chou-pei Suan-ching (Zhou Bi Suan Jing), which dealt with problems in Arithmetic, Algebra and Geometry (300BC). The most noted is the ancient manuscripts known as Chiu-chang Suan-shu (Jiu Zhang Suan Shu) which has 9 chapters with 246 problems on Algebra, Number Theory and Geometry (200BC).

Indian

In the literature, ancient Indian mathematics refer to the mathematics of the Indian subcontinent. The Indus or Harappan civilization existed at 3000BC in the Indus Valley of Pakistan. They have a system of weight and measure based on a decimal system. Many of the weights were of the shapes of cone, cuboid, cylinder, etc. They also have artistic drawings of concentric circles and triangles. Although the Vedic religion is believed to exist before 4000BC, significant link to mathematics (and astronomy) only came in around 2000BC. The Sulbasutra is a series of works dated from 800-200BC of the Vedic period. The sutra shows that the Indians work with irrational numbers, Pythagoras Theorem, certain quadratic equations. In the sutra can be found different values of π ranging from approx. 3 to 3.2. They did better in getting the value of √2, which is correct to 5 decimal places. Their results were of course all in fractions rather than decimals. The Arabic number system (1, 2, 3, ...) that we are now so familiar has its roots in Indian Brahmi numerals.

Greek

The Greek era of Mathematics started with Thales when he brought Egyptian Mathematics into Greece at 575BC and it lasted till 400AD. The Greeks made such great contributions to Mathematics that it shaped the future of Mathematics. As the years went pass, other civilizations made their contributions, these included the Mayans and Arabs.

Return to Maths Homepage