21th Century Mathematics: What's ahead of us?
As we enter the
21th century, I can't help but ask: has Mathematics reach its peak
yet? Are there new things to learn? Would there be new discoveries? The answer
is of course that new discoveries will keep pouring in and Mathematics still has
a long way to go. There are still sciences out there waiting for someone to give
them a full mathematical treatment; there are great many unsolved problems in
Mathematics; the implications of G�del's Theorems
are yet to be fully appreciated and utilised. As the fundamentals of Mathematics
are scrutinized and challenged, new discoveries will follow. Below is a list of
some mathematical problems I think is worth exploring. They are by no means
exhaustive, but should keep us busy for the whole of this century.
First of all, let's take a look at works to be done on the Foundation of
Mathematics in Problems 1 - 3.
1. Determination of Unprovable Statements
The most important
mathematical discovery in the 20th century are G�del's Theorems. We
learn from G�del that within any reasonably rich formal system there are
unprovable statements and if we try to incorporate these statements or their
negations as axioms, new unprovable statements will arise. So is all lost? Is
our present treatment of Mathematics to tumble down and get totally nullified?
The answer is an obvious NO. What G�del told us essentially is that we must know
the limitations of Mathematics. But this does not negate our formulation of
mathematical theories. A mathematical theory is acceptable as long as it fits
our experience, observations and knowledge. Of course, the theory must remain
rigorous and fully structural. The problem I'm proposing here is to
determine which statements in Mathematics are provable and which are
not.
G�del and Cohen have proven that the Continuum Hypothesis is unprovable
within the realm of Cantor's Set Theory. We know the Parallel Postulate in
Euclidean Geometry is also not provable and incorporating the various forms of
it as an axiom, we end up with various non-Euclidean Geometries. Perhaps there
are possibly algorithmic procedures to go about finding the unprovables. Another
question of interest is: are the unprovables high in occurrence in Mathematics?
2. Unification of Mathematics
We know many fields of Mathematics are
closely linked, like Arithmetic and Geometry. But there are others which have
no apparent relationship and yet sometimes unexpected applications from a field
can solve a difficult problem in another, e.g. Andrew Wiles' proof of
Fermat's
Last Theorem (FLT). Perhaps there are greater links between all fields of
Mathematics then we can imagine. Perhaps
the whole of Mathematics can be unified as one.
Actually, this problem is not new. Many mathematicians have work on it and
have achieved great success in unifying some fields. E.g. it is understood that
Algebra is Arithmetic in disguise; Topology is a Geometry in which the
requirements on the topological objects are less stringent than those of
Euclidean Geometry; that all numbers can be developed from counting numbers;
that the counting numbers are themselves definable in terms of Set Theory. In
particular, the whole of Mathematics can be built upon a framework of
Mathematical Logic. There is still much to do before a complete unification can
be achieved. Questions like how Statistics is related to Fuzzy Logic does not
have an evident answer. We know Fuzzy Logic is a generalization of the familiar
Binary Logic and that Statistical Theories hinges on Probability Theory, but
what's the profound link involved? My vision is that the whole of Mathematics is
related by a tree structure with Mathematical Logic as the root.
3. Metamathematics
One of the consequence of challenging the foundation
of Mathematics is the rise of Metamathematics. It all started with a whole host
of self-referencing statements in Mathematics, like the Liar's Paradox,
Russell's Paradox and the very statements G�del used to prove his famous
theorems. E.g. Liar's Paradox seeks an answer to the question "Is the statement
"I'm a liar" made by a liar or a truthteller?". It is evident that the statement
in the question is a self-referencing statement, because it refers to the
speaker himself. Similarly, questions regarding whether the set of all sets is
itself a set leads to the differentiation between sets and classes (Classes
being 'meta-sets'). Statements in Metamathematics are statement about
Mathematics; they are not statements within Mathematics. For example, the
statement "Geometry is consistent" is a statement about the structure of
Geometry, it is not itself a statement in Geometry. Metamathematics is a
language to describe the Mathematics we are interested in. They have their own
structure. So now the question: Is Metamathematics a field of Mathematics in its
own right? This is itself a question about Metamathematics and hence would
involve Metametamathematics. It seems that this could go on forever, unless we
are able to come up with a concrete theory to understand the whole mess. There
is more to Metatheories than we can imagine and concrete investigations into
their workings have to be made before we can understand Mathematics itself. For
a start we could start off by
unravelling the structure of Metamathematics.
We move next into the realm of Number Theory.
Until now, we still have yet to fully understand
the nature of Prime Numbers and it is difficult to determine the primality of
larger integers (this is presently used for coding purposes). There are great
many other unsolved problems in Number Theory (NT). Why is it that a simple
definition of the primes can lead to so many problems? The reason is that they
don't seem to follow any particular order. Order is an important element in
Mathematics; it is the very reason generalizations of problems are possible.
This is precisely why there are many extremely simple-to-state problems in NT
without easy solutions. In fact, many profound theorems in NT have to be proven
using theorems in other mathematical fields. Why is it that a problem in NT has
to find its proof elsewhere and not within NT itself? This is perhaps due to
G�del's Theorems or perhaps they can actually be proven within their own field,
just that more work needs to be done. These many questions may be resolved only
when we fully
unravel the mystery behind primes.
That's because all integers factorize uniquely into primes, a result known to
us as the Fundamental Theorem of Arithmetic. Much work has been done on primes
and some offer promising insight into the structure of primes. E.g. one of the
challenges in NT is to find a Prime Number Generating Function. In 1975, James
Jones solved this problem by giving a formula for generating the
nth prime, but it proves difficult to use when n gets
large. Another great problem regarding primes is about their distribution. Since
Gauss's
solution (the Prime Number Theorem) to this, there has been many refinements;
some utilizing the Logarithmic Integral, while others use more complicated
functions. All these are very encouraging, but more needs to be done.
Two particularly important long-standing problems in NT and their
significance are mentioned below.
5. Riemann Hypothesis
In the 20th century, the most important
unsolved problem in NT is FLT. Following Andrew Wiles' proof of FLT in 1994,
Riemann Hypothesis (RH) has risen to replace FLT. RH states that all the
non-trivial zeros of the zeta function have real part half. The reason this is so
has to do with the implications if RH is true and the importance of the Zeta
Function. In fact, the Prime Number Theorem (a major result in the field) can be
proven using the Zeta Function. Hence, RH could ultimately lead us to settle
problem 4 above. Also, RH finds application in apparently
unrelated fields, e.g. Chaos Theory. A recently proved theorem suggests the Zeta
Function may describe all the chaotic behaviour a quantum system exhibits.
Andrew Odlyzko has shown that the distribution of spacings between neighbouring
zeros tallies exactly with that between energy levels, if a chaotic system does
not exhibit symmetry.
6. Infinitude of Primes in Simple Expressions
Some of the outstanding
unsolved problems in NT has to do with
whether there are infinitely many primes in any given infinite
sequence.
The most prominent of which is Goldbach's Twin Prime Conjecture, which ask
whether there are infinite pairs of primes which differ by two. Generalization
of this conjecture led to the Prime AP Problem, which ask whether there are
infinite pairs of primes in any given Arithmetic Progression (AP) with first term,
a, and common difference, d. Non-AP type problems include, Sophie
Germaine Primes, Mersenne Primes, Fermat Primes, etc.
An unsolved problem in Algebraic Number Theory is Problem 7.
7. Determination of Rationality of Numbers
Presently there is no general
way of determining whether a number is rational or otherwise. The method used in
Euclid's
Elements for proving the irrationality of
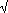2 has offered insight into a general proof of the
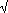irrationality of n for all integer
n greater than 2. Subsequently others have been proven irrational, famous
among these are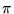 
and the base of natural
logarithm, e. But there remain others which rationality is still unknown.
Foremost among these is Euler's Constant. A more difficult problem to solve is
that on transcendentality. Transcendental Numbers are numbers which are not
solutions to any Algebraic Equation. Again it is known that
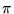and e are transcendental because being the
two most fundamental constants in Mathematics, there has been a great deal of
work on them. The challenge is to formulate an algorithm to
determine the rationality and transcendentality of any
number.
As computation, programming and computer logic in general are playing a
crucial role in present-day Mathematics, more emphasis needs to be put on them.
There has been much advances in this field since Alan Turing's effort to
formalize the notion of computation. Of particular importance is his proof of
the Halting Theorem in 1936. Generalization of the Universal Turing Machine
(developed by Turing, of course) has been made in the 1980s by Stephen Smale and
his colleagues, Lenore Blum and Mike Shub, via the BSS (Blum-Shub-Smale) model.
Of greater interest is a theory of computer programming (not just about
computations), we look at this and 3 other related problems below.
8. Computer Programming Problem
Presently, there are many programming
languages in the market. Among the most famous now is Java Programming. No
matter which language you may prefer, the common attribute for all of them is a
logical structure. The compiler is an essential part of computer programming
because it is used to check whether there are any syntax errors and basic logic
errors. For more subtle logic, the debugger comes in handy for those who are
familiar with it. And sometimes the logics can be so complicated that it
generates lots of errors which are difficult to detect. Particularly if the
program is very long, debugging is a big headache. Which programmer being given
programs written by others and asked to develop on them, had not found great
difficulties in comprehending what was written? All these problems arise due to
the lack of a standard set of logical foundations in programming. The challenge
here is to
draw up a mathematical structure for computer programming logic in
general.
Something like a set of axioms, from which specific results can be deduced.
These can then be applied to greatly reduce the complexity in programming.
Computers are here to stay and their effects on us will be unprecedented. We may
have to totally accept computational proofs of mathematical theorems in the
future. Take for example Kenneth Appel and Wolfgang Haken's solution to the
Four-colour Theorem. Even now there has been controversy whether that can be
called a 'proof'. It took the computer of the year 1976 about 1200 hours of
computer time to examine all the 1936 networks and hence no one would want to
spent his time verifying that all these cases are true. Although the
mathematical concept behind the computation is rigorous, there is no one to
verify the result. This problem can be solved if there is a clear presentation
of the logical structure of the program used to examine all the networks. So,
before we can really called it a 'proof', we have to ensure that the logical
structure of the program is sound; something achievable by formulating a
rigorous mathematical structure as proposed above.
9. P=NP Problem
This problem is with regard to Computation Theory. It
asks whether all problems whose answers can be checked in polynomial time (NP or
Non-deterministic Polynomial time) can actually be solved in polynomial time (P
or Polynomial time). Stephen Cook showed in 1971, that a lot of the NP problems
are equivalent, thus all that is required is to find a single NP problem that is
not in P. By 1998, no more than 1000 NP problems have been indentified. Although
thought to be false, until now no one has been able come up with a
counterexample.
10. Regular-patterned Iterations
Imagine the following simple algorithm:
1. Start with any positive integer, n.
2. If it is even, divide by 2; if
it is odd, multiply by 3 and then add 1.
3. go back to 2.
It is conjectured that the resulting sequence always end in 4, 2, 1, 4, 2, 1,
... But no one has yet to prove (or disprove) this. Again the question arises
why such a simple algorithm can result in such a difficult problem. Perhaps the
greater question is
which simple algorithms result in a regular-patterned ending
sequence?
11. Mathematics Software
This problem may seem inappropriate to be
mentioned here, but I believe it is no less important. The problem I propose
here is to
develop softwares for all fields of Mathematics.
Of course, I'm not asking for a 'truth machine' here. We know from the
Halting Theorem that no such machine exists. What I talking about are softwares
out there, like Mathematica and Matlab, which help us in dealing
with difficult problems. Some of these are so powerful that they can demonstrate
origami (the art of paper folding), produce real-life graphics from
various perspectives, and manipulate complicated functions (e.g. Bessel
Function). This is good and bad news. First the bad news. Over-reliance on
softwares results in reduced understanding of the concepts involved and lack of
admiration of the beauty of Mathematics. That's because the step-by-step
deduction of a problem is performed by the computer and so the user has no need
to work through the steps involved. This over-reliance is actually highly
evident all around us. It started with the invention of the pocket calculator. I
have seen great many people punching on the calculator when asked to perform a
simple addition; and they can't recall the value of sin30o,
without a calculator.
On the other hand, we can't do without these softwares. How do you perform
millions of iterations without a computer? How can we find approximate solutions
to the Wave Equation without several hours (or days) of simulation? How can we
manipulate a gigantic matrix without a computer? Watching topological
transformations unfolding (or folding, in the case of origami) in front of our
eyes is a great learning experience. There are many things a good computer
software can do to help us in our learning of Mathematics. In fact, they are
indispensible insofar as dealing with complicated problems.
The important thing to note then is to try and instill in the minds of our
children the importance of logical deductions and the actual role of softwares.
Another thing that needs improvement is a lack of an easy way to present
Mathematics on the Internet. The HTML format does not facilitate editing of
formulas and drawing of simple objects, which are much needed in a presentation
of mathematical theories. What's needed is a HTML toolkit for Mathematics.
We proceed next to applications of Mathematics to the observed phenomena in
the world (Problem 12). Of the multitude of phenomena in our world, there remain
many which we do not comprehend as yet, as well as, others which we are fairly
capable of explaining. No matter which category a phenomena is in, it is my
contention that all can be given a suitable mathematical treatment. Related
problems are described in Problems 13 and 14 . In these, I'll discuss how Chaos
Theory and Complexity Theory, and the study of Randomness allows us to
understand the many existing phenomena.
12. Mathematical Treatment for All Phenomena
There are many places in
the world where Mathematics are indispensible. There are also places where you
least expect Mathematics to exist and yet it just cropped up from nowhere. E.g.
who would expect Mathematics to find its way into Knot Theory, artistic designs,
a queen bee's hive, just to name a few. Mathematics is obviously everywhere.
Even so, there are still many systems in which no proper mathematical theory has
been incorporated. On top of this, there are others in which a mathematical
treatment exists, but the treatment is not fully rigorous. More work ought to be
done on the rigor of such mathematical models. It is hope that researchers in
their own specialized fields will provide such a structure to their own field of
specialization. In addition, it is hope that those systems as yet without a firm
mathematical structure be given one. Of course this will depend on how well
human beings understand the systems. Among these are Darwinian Evolution,
twister formation, earthquakes, etc. There has been much work on them, e.g. in
explaining the relationship between living things, predicting when twisters will
form, when earthquake are expected, etc. This is encouraging. The more we
understand them, the better we can come up with a suitable model. Presently with
the information at hand, we can draw up a basic mathematical structure for each
of them and incorporate new discoveries as and when they arise. The vision is
that
all phenomena be given rigorous mathematical treatment where
possible.
13. Chaos Theory and Complexity Theory
Chaos Theory has
to do with simple things getting complicated, whereas Complexity Theory has to
do with the exact opposite, i.e. order and pattern in complicated things. Both
are recent Sciences (or Mathematics, depending on how you look at it) and both
are capable of explaining the many phenomena we see in the world. Within the
last 30 years, many scientists and mathematicians have contributed greatly to
Chaos Theory. Among them are Edward Lorenz, David Ruelle, Floris Takens, Robert
May, Jack Wisdom, Mitchell Feigenbaum, Michel H�non and Stephen Smale. Chaos is
everywhere, from biology to astronomy to economics, you name it, you get it. A
good understanding for chaos is lacking presently, more has to be done.
Complexity is like an inverse of Chaos, perhaps there is a greater connection
between the two. Complexity has applications in fields like Neural Network, etc.
Both these theories have great potential in unravelling the many mysteries in
this world. However, the many discoveries in these theories are isolated pieces
of the full picture. A great deal of work still remains to patch the pieces
together and to obtain a
formulation for Chao Theory and Complexity Theory.
14. Understanding Randomness
Many theories have been introduced to
describe randomness. Since Pascal
and Fermat's founding of Probability Theory, we have more understanding of
random events. And the various statistical theories have been helpful in
describing random occurrences. Recently, Kolmogorov Complexity allows us to
understand random events by observing the order surrounding them. It is seen as
an application of the dual principle, which keep cropping up in many fields of
Mathematics. Unravelling randomness is important for understanding random
events, e.g. stock market fluctuations, random number generation. But as too
many factors affect a system, randomness sets in and there is no way to predict
what will happen next. This leaves us with a very bad situation, as we can only
depend on our luck to help us. But if we do have a means of understanding
randomness, then we can have better control of the systems we are describing.
Furthermore, proper understanding of phenomena such as Small World Theory (huge
network of things are somehow linked to one another) and Murphy's Law (anything
that can go wrong, will go wrong), would depend greatly on
understanding randomness.
Next, we take a peep at Geometrical and Topological ideas and several
problems involved.
15. Poincar� Conjecture
The Poincar� Conjecture is an important
solved problem in Topology. It states that any simply-connected
three-dimensional (3D) manifold must be deformable to a 3D sphere in a manner
that allows no cutting or gluing.
16. Further Developments in Graph Theory
Graph Theory first appeared
with Euler's
solution to the K�nigsberg Bridge Problem, but there are a multitude of work on
the field only in recent decades. Although developed independently of Group
Theory, it has now become intertwined with the latter. There are many
outstanding conjectures in the field. One of these is "there is a hamiltonian
cycle in every Cayley graph." It is understood that this problem, if true, may
be solved just like the problem on the Classification of Simple Groups, i.e. by
considering many special cases and combining all these cases to form the
complete proof. There are many other conjectures awaiting mathematicians to
bring to light and it is certainly one of the richest fields at present. The
challenge is to
obtain a full development of Graph Theory.
Last of all, I would like to propose several, perhaps unrealistic but no
doubt interesting, problems. With an inquisitive mind, human beings are able to
dominate the Earth (and beyond). And it is precisely this curiosity that helped
Mathematics to blossom to its present state. Would the Irrational Numbers be
accepted if not for questioning the Pythagorean concept of numbers (i.e. all
numbers could be expressed as ratio of integers)? Would Einstein discover
General Relativity, if not for doubts in the Classical Theory? Major
breakthroughs in this world came from questioning the present state of
understanding and asking what lies beyond this state. Such is the desire for
generalization that new concepts keep pouring in. And so, pardon my probe into
the following realms beyond present-day Mathematics.
17. Beyond Topology
To the ancient Greeks, Euclidean Geometry describes
everything in the universe. However, unknown to them, the world is only
Euclidean in the approximate sense. For example, the surface of the Earth is
actually Spherical Geometry in nature, but if you look at a small region, the
spherical surface can be approximated by an Euclidean one. There are other forms
of non-Euclidean Geometry, like Hyperbolic, Elliptic and Projective Geometries.
Topology or 'rubber-sheet' Geometry was first discovered by Euler and Fractal
Geometry is formulated by Benoit Mandelbrot. It seems that there may still be
other Geometries unknown to us at present. In fact, a minute of thought would
lead us somewhere. Topology does not allow cutting and gluing of geometrical
objects. Suppose we are allowed to do these, what type of Geometry would we get?
The answer is Quantum Geometry, which get its name from a quantum mechanical
effect. Brian Greene, David Morrison and Andrew Strominger have shown that
quantum effects make it possible for spaces of different numbers of holes to
transform smoothly onto one another. E.g. a torus can be tranformed into a
sphere. So the challenge here is to
investigate Quantum Geometry and other possible new
Geometries.
18. Complex Dimension
Integer dimensions are not foreign to all of us,
in particular, we are familiar with n-dimensional (nD) objects,
where n = 1, 2 or 3. Higher dimensions are understood as nD
vectors. Also, we know the 0D object is a point. And from Fractal Theory, we
know of the existence of non-integer dimensions. In general, to multiply the
size of a d-dimensional (dD) hypercube by a factor of a, you need
c = ad copies, so d = logac.
Naturally, the question arises
what are negative-dimensional objects; further, what about complex
dimensions?
19. Beyond Quaternions
Because of man's desire to generalize, we
advanced from the simple Whole Numbers to the Rationals, the Reals and the
Complex. The Reals can be viewed as 1D numbers, while the Complex can be seen as
2D numbers. So the question that Hamilton asked was what about higher
dimensional numbers. His search for 3D numbers ended in failure, but he invented
the 4D numbers (Quaternions) in 1843. Like the discovery of new types of numbers
throughout history, initially, everyone is skeptical about the new types of
number. But subsequently, these numbers find their place in real life and are
then accepted. The quaternions took the same path and were given the cold
shoulder at first, but now finds applications in our life. One of these being
their uses in communicating graphics information on computers by giving
description of rotations in 3D. The question that naturally arises now is
whether there exist numbers beyond quaternions.
Return to Maths Homepage